Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 37
37. Use a análise de malhas para determinar as correntes , e no circuito da figura
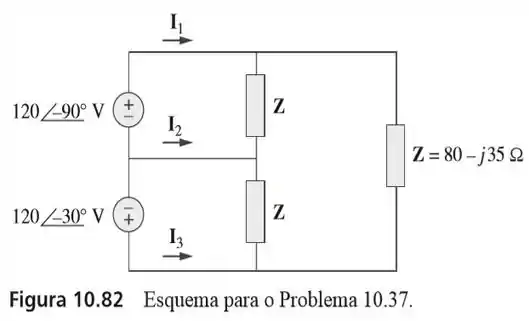
Passo 1
Fala galerinha! Vamos pra mais um problema sobre circuitos com corrente alternada.
Olha só! A questão foi boazinha com a gente e já nos deu todos os seus elementos na forma fasorial.
Bom pra gente, né não! Bora partir logo pra análise de malhas!
Passo 2
Nesse passo, vamos preparar o circuito pra utilizar a nossa análise de malhas. Quando digo preparar, é simplesmente nomear as correntes de malha!
E bora lá reformular esse circuito. Aqui está nossa bela figura:
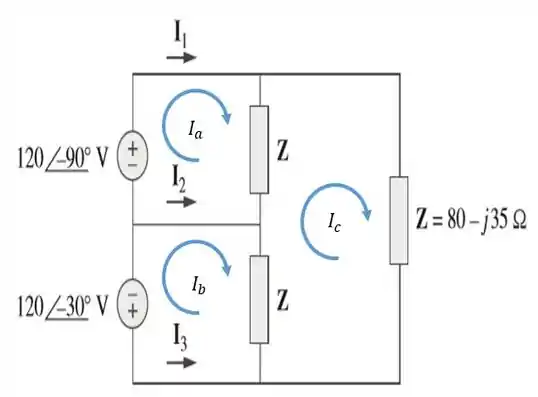
Diante disso... Bora aplicar a lei das tensões de para a malha :
Depois, bora partir pra análise da malha :
E por último a análise da malha :
Passo 3
Precisamos resolver assim, o seguinte sistema:
Que pode ser escrito na forma matricial, como:
Mas a questão pede pra gente usar o , né!
Só que a gente não tem! Xiiii
Calma! Não criemos pânico! Como não temos disponível, vamos usar um outro software bastante comum na graduação dos alunos de engenharia e que se assemelha muito ao . É o .
Olha só! O sistema matricial anterior é fornecido através de três matrizes. Vamos dar nomes a elas:
A solução desse sistema, que é a matriz , é dada no pelo produto da inversa de por . Desse modo:
Só que temos que adaptar essas matrizes à linguagem desse software.
A matriz fica assim:
E a matriz :
O reconhece o , que é a tradicional notação da forma retangular, como . Sendo assim, colocando os dados no software, obtemos as seguinte respostas:
E olhando a figura do enunciado, podemos ver que as correntes , e são dadas por: