Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 58
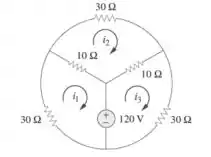
58. Determine i1, i2 e i3 no circuito da Figura 3.103
Passo 1
Vamos usar a analise de laço, o exerciocio já atribuiu as correntes de malha, então o primeiro passo da analise já esta feita.
Passo 2
Vamos aplicar a LKT (a soma das quedas de tensão de uma malha deve ser igual a zero) em cada uma das malhas.
Primeiro percorrendo a malha 1:
Dividindo por 10:
A malha 2:
Dividindo por dez:
E por fim, a malha 3:
Dividindo por dez:
Passo 3
Agora é só resolver o sistema, podemos usar o MATLAB, uma calculadora, algum outros software, ou até mesmo fazer na mão.
Montando esse sistema com matrizes:
Resolvendo o sistema:
Resposta
Exercícios de Livros Relacionados
37. Resolva o problema 3.8 , usando análise de malhas.
38. Aplique análise de malhas ao circuito da Figura 3.85 e obtenha I 0 .
39. Usando a figura 3.50 do problema 3.1 , elabore um problema para ajudar outros estudantes a entenderem melhor a análise de malhas.
40. Para o circuito em ponte da Figura 3.86 , determine i 0 usando análise de malhas.
42. Usando a figura 3.88 elabore um problema para ajudar estudantes a entenderem melhor a análise de malhas usando matrizes.