Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 59
59. Refaça o Problema 3.30, usando a análise de malhas.
Passo 1
O exercício 3.30 queria que nós encontrássemos e . Para usar a analise de malha vamos atribuir as correntes de malha, como temos uma fonte de corrente entre duas malhas precisamos definir uma supermalha que está circulada de amarelo:
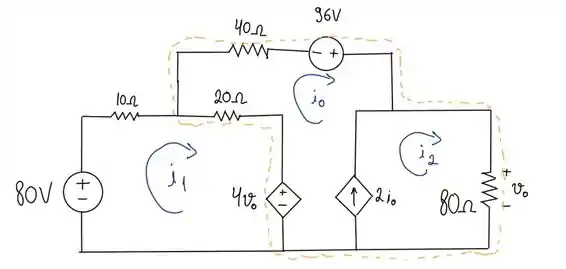
Passo 2
Podemos iniciar a analise montando a equação interna da supermalha, quando as correntes e se encontram elas devem ser iguais ao valor da fonte de corrente que esta dentro da supermalha:
Então vamos aplicar a LKT (a soma das quedas de tensão de uma malha deve ser igual a zero) percorrendo a supermalha por fora:
Dividindo por 4:
Nós sabemos, olhando para o circuito que
Substituindo na equação:
Simplificando ela:
Analisando a Malha 1:
Substituindo o :
Dividindo por 10:
Simplificando a equação:
Passo 3
Agora é só resolver o sistema, podemos usar o MATLAB, uma calculadora ou algum outro software:
A matriz vai ficar dessa forma:
Resolvendo:
Já descobrimos a corrente , agora falta a tensão . Pela lei de ohm podemos escrever ela como:
Como já descobrimos a corrente :