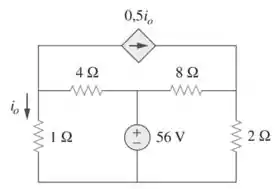
60. Calcule a potência dissipada em cada resistor no circuito da Figura 3.104.
Passo 1
Eaee, tranquilinho?? O enunciado nos deu o seguinte circuito:
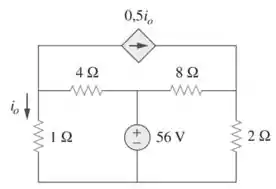
Queremos calcular a potência dissipada em cada resistor.
Para isso, devemos saber que a potencia dissipada em um resistor pode ser expressa dessa maneira:
Então se encontrarmos as correntes que passam nos resistores, encontramos a potencia dissipada.
Podemos usar a analise de malha, então devemos atribuir as correntes de malha do circuito, vamos dizer que a corrente da malha de cima (malha 1) é , a corrente da malha da esquerda de baixo (malha 2) é e a corrente da malha da direita (malha 3) é . Lembrando que as correntes de malha estão sempre no sentido horário.
Passo 2
Como esse circuito possui uma fonte de corrente, que só pertence a uma malha, podemos escrever que:
Podemos observar também, que:
então,
Agora vamos aplicar a LKT (a soma das quedas de tensão de uma malha deve ser igual a zero) percorrendo a malha 2:
Simplificando:
E só faltou aplicar a LKT na malha 3:
Simplificando:
Passo 3
Agora é só resolver o sistema, podemos usar a calculadora, o MATLAB, ou algum outro software.
Montando na forma de matriz:
Resolvendo o sistema:
Passo 4
Agora que descobrimos as correntes é só calcular a potencia dissipada em cada resistor:
Resistor de 1 ohm:
Resistor de 2 ohms:
Resistor de 4 ohms:
Resistor de 8 ohm: