Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.9 - Ex. 2
Demonstre que o circuito dado e equivalente a rede reciproca genérica de três terminais, mostrando que (14.38) se aplica.
Passo 1
Iae, meus queridos! Td certinho??
Essa questão é bem tranquilinha, confia no pai 😉
Temos o seguinte circuito:
E as seguintes equações:
Ou
No enunciado ele pede pra mostrar que o circuito é equivalente à rede recíproca genérica de três terminais, ou seja, ao aplicarmos as condições das equações acima, temos que encontrar os valores das admitâncias descritas.
Por ser uma rede reciproca genérica de três terminais, .
Passo 2
Quando , significa que os terminais de estão em curto. Ou seja...
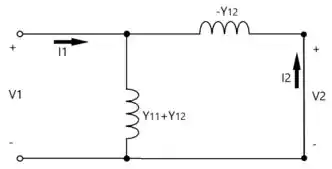
Primeiro, vamos encontrar uma relação entre e , pra isso, podemos dizer que é igual a soma das correntes que flui pelos dois braços, com os quais possuem o mesmo potencial .
Primeira condição encontrada.
Com o mesmo circuito, temos que encontrar uma relação entre e , pra isso podemos aplicar a lei de Ohm na admitância .
OBS: o sinal negativo no lado direito da igualdade se dá pelo fato do sentido da corrente percorrer o sentido oposto da convenção.
Segunda condição encontrada.
Passo 3
Quando , significa que os terminais de estão em curto. Ou seja...
Faremos os mesmos procedimentos do passo anterior pra encontrar as condições necessárias.
Admitindo que é a soma das correntes dos braços do circuito cuja tensão é .
Terceira condição encontrada.
Para encontrar a relação entre e , aplicamos a lei de Ohm na admitância .
Quarta e ultima condição encontrada, com isso, demonstramos que o circuito dado é equivalente à rede recíproca genérica de três terminais.
Achou fácil? Tenho ctz que tirou de letra.
Resposta
Demonstração no passo-a-passo.