Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 63

63- Determine I_o no circuito da Figura 11.82

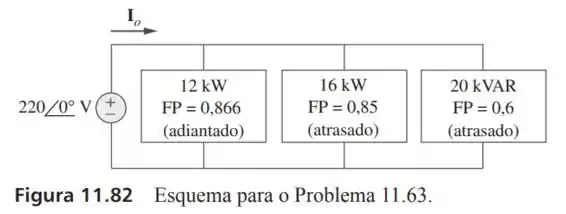
Passo 1

Nesse exercício podemos calcular a corrente somente calculando a potência total do sistema. Diferente da 62 onde tínhamos que nos preocupar com outras variáveis.

Começando pela carga com F P = 0.866 com carga de reatância capacitiva.

S = P +- j (P)/(F P) sqrt(1 - cos^2 theta)

Onde cos theta = F P

S_1 = [12 - j (12)/(0.866) sqrt(1 - 0.866^2)] k V A = [12 - j 6.929] k V A

Agora a carga com F P = 0.85

S_2 = [16 + j (16)/(0.85) sqrt(1 - 0.85^2)] k V A = [16 + j 9.92] k V A

Agora para a última carga:

S = [(20)/(sqrt(1 - 0.6^2)) xx 0.6 + j 20] k V A = [15 + j 20] k V A

Isso nos dá uma potência total igual a:

S = S_1 + S_2 + S_3 = [43 + j 22.991] k V A = 48.76 /_ 28.13 ° k V A

Passo 2

Então a corrente será calculada por:

I_(R M S)^* = (S)/(V_R M S) = (48.76 k /_ 28.13)/(220 /_ 0) = 221.64 /_ 28.13

Então:

I_R M S = I_o = 221.64 /_ - 28.13 ° A

Resposta

I_o = 221.64 /_ - 28.13 ° A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O valor de pico da tensão da fonte senoidal do circuito da Figura P10.48 é 180 V, e sua frequência é 5.000 rad/s. O resistor de carga pode variar de 0 a 4.000 V e o capacitor de carga pode variar de 0
a) Determine a relação de espiras N1/N2 do transformador ideal, no circuito da Figura P10.63, de modo que uma potência média máxima seja fornecida à carga de 400 V. b) Determine a potência média forne
A impedância ZL no circuito da Figura P10.54 é ajustada para máxima transferência de potência média a ZL. A impedância interna da fonte de tensão senoidal é 4 + j7 V. a) Qual é a máxima potência média
O resistor de 160 V no circuito da Figura P10.51 é substituído por uma impedância variável Zo. Admita que Zo seja ajustada para transferência de máxima potência média. a) Qual é a máxima potência médi
Determine a expressão de regime permanente para as correntes i g e i L no circuito da Figura P10.55, quando vg = 400 cos 400t V.Determine o coeficiente de acoplamento. c) Determine a energia armazenad