Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 67
67- Para o circuito com da Figura , calcule:
A potência complexa liberada pela fonte de tensão.
A potência média dissipada no resistor de .
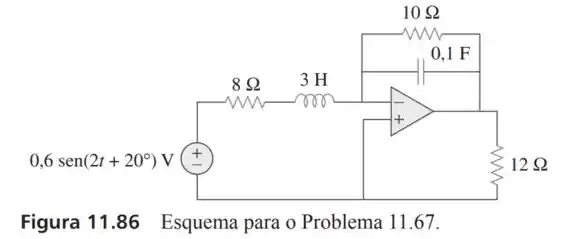
Passo 1
A fonte que não está em excita o circuito com uma velocidade angular igual a:
Com o fasor da tensão não sendo igual a:
Logo a reatância do capacitor e do capacitor serão iguais a:
Não sei se você lembra, mas esse esquema representa um amplificador inversor que tem a seguinte forma:
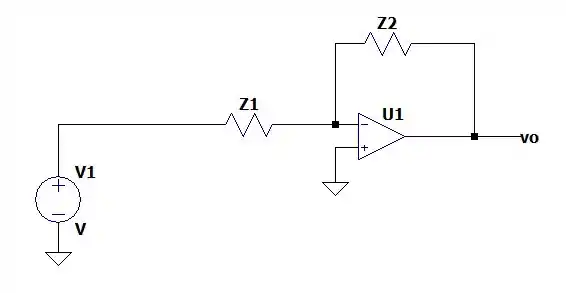
E tem a seguinte relação entre a tensão de saída com a de entrada:
E essas impedâncias no circuito da nossa questão serão iguais a:
Passo 2
Vamos desenhar nosso circuito.
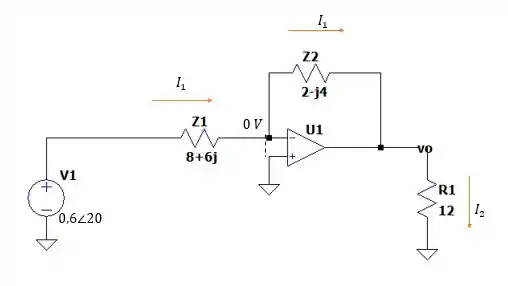
Sabendo que a tensão na porta inversora é e que a potência aparente liberada pela fonte (Não ) será de:
Então podemos calcular pela diferença de tensão entre a fonte e a tensão na porta inversora, sendo igual a:
Então a potência complexa será igual a:
Passo 3
Para fazer a letra vamos calcular a tensão de saída no amplificador operacional:
Então a potência complexa será:
Uma vez que a reatância na verdade é uma resistência. Nos dando então uma potência real.