Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 27
Considere o circuito descrito no Problema 9.78.
a) Qual é o valor eficaz da tensão na carga?
b) Qual percentagem da potência média produzida pela fonte real é fornecida à carga?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Primeiramente, o indutor mútuo tem uma impedância igual a
Temos a seguinte configuração de circuito para este caso
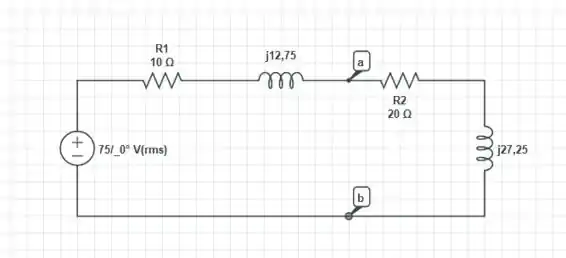
A impedância equivalente visto através dos terminais a, b mostrados no circuito é dado por
Determinando a corrente fluindo através do indutor
Transformando em fasores,
Passo 2
A impedância do lado secundário do transformador é dado por
Determinando a corrente fluindo através do transformador secundário
Substituindo os valores, nós temos que
Simplificando um pouco mais as coisas
Com isso, nós temos que
Determinando a tensão aplicada na impedância da carga
Com isso, nós obtemos que
Transformando em fasores, nós temos
A magnitude será igual a
Passo 3
B - Determinando a potência média ideal fornecida pela fonte de tensão,
Com isso, nós temos que
Agora, vamos determinar a potência média dissipada na impedância interna da fonte no caso prático,
Substituindo o , nós temos que
A potência média fornecida pela fonte de tensão prática,
Logo,
Agora, a potência média fornecida pela impedância da carga
Novamente, substituindo os valores
Determinando a porcentagem da potência média entregue à carga daquela fornecida pela fonte de tensão prática, nós temos que
Com isso
Portanto,