A questão descreve um circuito que está a bastante tempo em um estado, o que ela quer que você saiba, é a mudança de comportamento do circuito a partir da abertura da chave. Portanto, let’s go e vamos resolver!
Passo 1
A - Para t

Então, a corrente que está “saindo” da fonte é igual a:
Fazendo o divisor de corrente, temos:
Para t > 0, como é que fica?
Como o indutor não pode variar a corrente instantaneamente, senão sua derivada iria corresponder a uma tensão infinita, então temos a seguinte relação matemática.
Graficamente, o circuito se comportaria da seguinte forma:
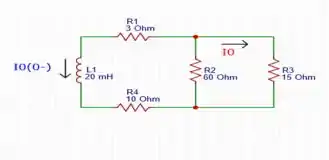
Logo, a corrente para um instante t é dada pela seguinte equação:
Agora, é encontrar o e substituir os termos.
Lembre-se que é a soma entre o resistor de 3 ohms e o paralelo com o de 60 e 15. Fazendo os cálculos, têm-se:
E o seu inverso:
Com isso, temos a equação para um dado instante de tempo t:
Passo 2
B – Aqui o negócio é lembrar da tensão no indutor e qual é sua fórmula, e depois fazer um divisor de tensão.
A fórmula para o divisor de tensão é esta aqui:
Como já temos , agora é só substituir e derivar, ficando com esse resultado aqui:
Fazendo mais alguns cálculos, temos:
E temos a tensão no indutor!
Para o cálculo de , temos que fazer um divisor de tensão:
Substituindo o
E finalmente