Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 90
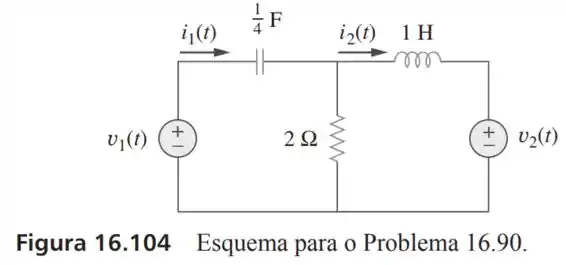
90- Desenvolva as equações de estado para o circuito mostrado na Figura
Passo 1
As variáveis de entrada são e e as variáveis intermediárias são a tensão no capacitor e a corrente que passa pelo indutor . Desenhando algumas variáveis no circuito nós teremos:
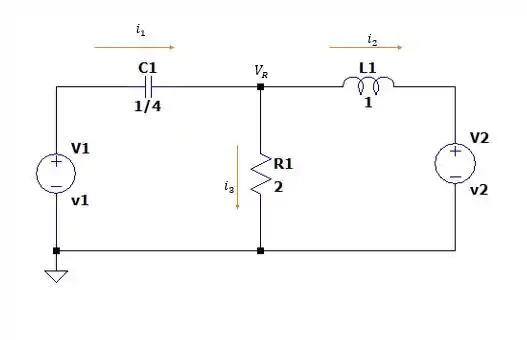
Somando as correntes nós temos:
Então a tensão no resistor será:
A tensão no capacitor será:
A corrente que passa pelo capacitor será:
E a tensão no indutor será:
Passo 2
O que precisamos escrever na equação de estados é:
Só que
Então:
A parte de está arrumada, agora vamos para , juntando com a equação temos
Só que já sabemos o resultado de :
Então a nossa equação de estado fica:
Passo 3
Agora para a equação de saída:
Falta uma equação para e podemos escrever pela equação de em :
Então a matriz fica:
Resposta
Exercícios de Livros Relacionados
Calcule as integrais a seguir envolvendo as funções de impulso: a∫ - ∞ ∞ 4 t 2 ⋅ δ t - 1 d t b∫ - ∞ ∞ 4 t 2 ⋅ cos 2 π t ⋅ δ t - 0.5 d t
Esboce a forma de onda representada por i t = r t - r t - 1 - u t - 2 - r t - 2 + r t - 3 + u t - 4
Calcule as integrais a seguir: a∫ - ∞ ∞ e - 4 t 2 ⋅ δ t - 2 d t b∫ - ∞ ∞ [ 5 ⋅ δ t + e - t ⋅ δ t + cos 2 π t ⋅ δ t ] d t
Expresse v t na figura 7.105 em termos de funções degrau.
Expresse os sinais da figura 7.104 em termos de funções de singularidade.