Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 75
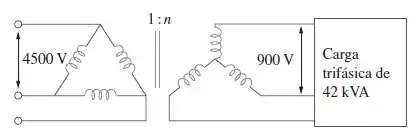
Um banco de transformadores trifásicos equilibrado com conexão triângulo-estrela representado na Figura é usado para abaixar tensões de linha de para . Se o transformador alimenta uma carga de , determine:
- A relação de espiras para o transformador
- As correntes de linha no primário e secundário
Passo 1
Galerinha, vamos para a letra (a). nós podemos encontrar a relação de espiras através da equação que relaciona as tensões primária e secundária do transformador. Como temos uma conexão ,
Substituindo os valores, temos:
Passo 2
A potência parente total do transformador pode ser escrita como:
Vamos achar primeiro a corrente de linha no primário:
Agora, a corrente de linha no secundário:
Resposta
- e
Exercícios de Livros Relacionados
37. Um transformador elevador de tensão ideal de 480 / 2.400VR M S libera50k W para uma carga resistiva. Calcule:(a) A relação de espiras. (b) A corrente no primário. (c) A corrente no secundário.
36. Conforme feito na Figura 13.32 , obtenha as relações entre as tensões e correntes nos terminais para cada um dos transformadores ideais da Figura 13.105 .
39. Um transformador de 1.200 / 240VR M S tem impedância 60 ∠ - 30 °Ω no lado de alta tensão. Se o transformador for conectado a uma carga de 0,8 ∠ 10 °Ω no lado de baixa tensão, determine as corrente
38. Um transformador de 4,6k V A , 2300 / 115V , 60H z foi projetado para ter uma f . e . m induzida de 2,5V o l t s / e s p i r a . Supondo o transformador ideal, calcule:a) O número de espiras do en
40. O primário de um transformador ideal com relação de espiras igual a 5 é conectado a uma fonte de tensão com parâmetros de T h é v e n i n é V T h = 10c o s2.000 tV e R T h = 100Ω . Determine a pot