Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 31

Altere em escala o circuito do Prob. 15.23 para obter um filtro passa-altas com ω c = 10 5 r a d / s , usando capacitores de 1 - n F (Sugestão: ω c  = 1 r a d / s no Prob. 15.23 .)

Passo 1

O enunciado pede que a gente altere em escala o circuito do Prob. 15.23 para obter um filtro passa-altas com ω c = 10 5 r a d / s , usando capacitores de 1 - n F . Vamos começar esboçando o circuito, vem comigo 😊

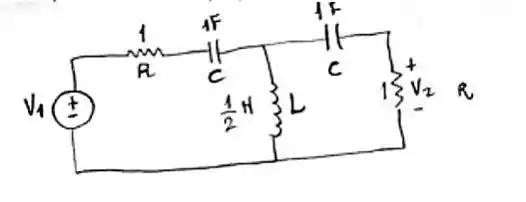
Fato 2

ω c = 10 5                           C = 1 n f

V 2 = R V R 1 / b C + R = R V e 1 + s R C s C ⇒ V 2 = s R C V e 1 + s R C ⇒ V 0 = V 2 ( 1 + s R C ) s R C

V 1 - V R + 1 / s C = V s L + V 1 / s c + R ⇒ V 1 = R + 1 / s C V 1 R + 1 / s + 1 s L + 1 s c + l ⇒

⇒ V 1 = V 2 + 1 + s R C s 2 L C ⇒ V 1 = V 2   2 + 2 s R C s R C + ( 1 + s R C ) 2 s 3 R L C 2

⇒ V 1 V 2 = s 2 L C ( 2 + 2 s R C ) + ( 1 + s R C ) 2 s 3 R L C 2 ⇒ V 2 V 1 = s 3 R L C 2 2 s 2 L C + 2 s 3 R L C 2 + 1 + 2 s R C + s 2 R 2 C 2

Passo 2

ω c  inicial = 1  rad /s K f = 10 5

ω c Final 10 5  rad/s

C = C ' K f K i ⇒ 10 - 9 = 1 10 5 K i ⇒ K i = 1 10 - 4 = 10 4

L = K i L ' K f = 10 4 1 / 2 10 5 = 0,05 H

R = K : R ' = 10 4 ⋅ 1 = 10 k Ω

Resposta

10 k Ω

Exercícios de Livros Relacionados

Calcula v 1 da equação diferencial e use o resultado para calcular a resposta forçada para v para uma tensão de entrada de 34 cos ⁡ 4 tV .
Calcule as representações fasoriais das funções no domínio do tempo (a) 10 cos ⁡ ( 5 t + 18 ° ) , (b) - 8 cos ⁡ 5 t + 6 sin ⁡ 5 t , (c) 18 sin ⁡ 5 t e (d) - 2 sin ⁡ ( 5 t - 10 ° )
Calcule R e L na Fig. 10.4, se a fonte é 13 cos ⁡ 6000 tV e a resposta é i = 2 cos ⁡ ( 6000 t - 67,4 ° )m A . (Tome tan ⁡ 67,4 ° = 12 / 5 ) .
Calcule as representações fasoriais das funções no domínio do tempo (a) 10 cos ⁡ ( 5 t + 18 ° ) , (b) - 8 cos ⁡ 5 t + 6 sin ⁡ 5 t , (c) 18 sin ⁡ 5 t e (d) - 2 sin ⁡ ( 5 t - 10 ° )
Na Fig. Do Ex. 10.2.2, se a fonte é 6 cos ⁡ 4000 tm A e a saída é v = 18 cos ⁡ 4000 t - 53,1 °V , calcule R e C.