Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 55

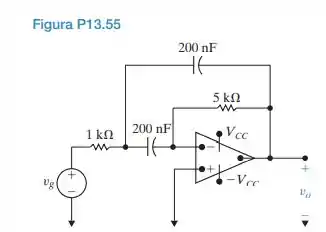
O amplificador operacional no circuito da Figura P13.55 é ideal.

a) Determine a expressão numérica para a função de transferência H(s) = Vo/Vg para circuito na Figura P13.55.

b) Determine o valor numérico de cada zero e polo de H(s).

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

  1. Desenvolvendo o circuito acima, temos que:

    2. Disso, tiramos:

    V a - V g 1000 + s V a 5 x 10 6 + V a - V 0 s 5 x 10 6 = 0

    Colocando Vg em função de Va e V0, temos que:

    - s V a - 1000 V 0 = 0

    Colocando Va em função de V0 e desenvolvemos. Chegamos em:

    V 0 V g = - 5000 s s 2 + 2000 s + 5 x 10 6

    Agora desenvolvendo s, temos:

    s 1,2 = - 1000 ± 10 6 - 5 x 10 6 1 2 = - 1000 ± j 2000

    Portanto:

    V 0 V g = - 5000 s ( s + 1000 - j 2000 ) ( s + 1000 + j 2000 )

    Passo 2

  2. Dados os conhecimentos que adquirimos no item acima, temos que:

z 1 = 0

- p 1 = - 1000 + j 2000

- p 2 = - 1000 - j 2000

Resposta

  1. Item a:

    2. V 0 V g = - 5000 s ( s + 1000 - j 2000 ) ( s + 1000 + j 2000 )

  2. Item b:

z 1 = 0

- p 1 = - 1000 + j 2000

- p 2 = - 1000 - j 2000

Exercícios de Livros Relacionados

Espera-se que um circuito ressonante R L C em paralelo tenha uma admitância de faixa média igual a 25 ×10 - 3S , um fator de qualidade 80 e uma frequência de ressonância 200 k r a d s . Calcule os val
Um circuito R L C em paralelo é ressonante em 5,6M H z , tem um fator Q igual a 80 e um ramo resistivo de 40 k Ω . Determine os valores de LeC nos outros dois ramos.
Um circuito ressonante em paralelo tem resistência de 2k Ω e frequências de meia potência de 86k H z e 90k H z . Determine:(a) A capacitância.(b) A indutância.(c) A frequência de ressonância.(d) A lar
Considere o circuito “tanque” da F i g u r a14.79 e determine a frequência de ressonância
Projete um circuito R L C ressonante em paralelo com ω 0 = 10 r a d s e Q = 20 . Calcule a largura de banda do circuito. Considere R = 10 Ω .