Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 36

Espera-se que um circuito ressonante R L C em paralelo tenha uma admitância de faixa média igual a 25 ×   10 - 3   S , um fator de qualidade 80 e uma frequência de ressonância 200 k r a d s . Calcule os valores de R ,   L   e   C . Determine a largura de banda e as frequências de meia potência.

Passo 1

Primeiro vamos relembrar que admitância, é o inverso da impedância.

A d m i t â n c i a = 1 I m p e d â n c i a  

Também vamos relembrar as relações fundamentais de um R L C em paralelo na resposta de frequência:

Q = R ω 0 L = ω 0 C R = ω 0 B

Sabendo que:

ω 0 = F r e q u ê n c i a   a n g u l a r   d e   r e s s o n â n c i a    

Q = F a t o r   d e   q u a l i d a d e  

R = R e s i s t ê n c i a   é l e t r i c a

L = I n d u t â n c i a   é l e t r c i a

C = C a p a c i t â n c i a   é l e t r i c a

B = L a r g u r a   d e   b a n d a

Por fim quando Q ≥ 10 , as frequências de meia potência podem assim ser expressas:

ω 1 ≅   ω 0 - B 2               e               ω 2 ≅   ω 0 + B 2

Passo 2

Vamos iniciar encontrando R

Sabemos que

A d m i t â n c i a = 1 I m p e d â n c i a

Então,

25 ×   10 - 3   S = 1 I m p e d â n c i a

I m p e d â n c i a = 40   Ω

Logo,

R = I m p e d â n c i a = 40 Ω

Como a admitância só contem uma parte real, a impedância também, só conterá uma parte real, essa parte real é exatamente o valor de R . Se vc estiver com dúvidas sobre os termos e as operações, esse esquema pode lhe ajudar:

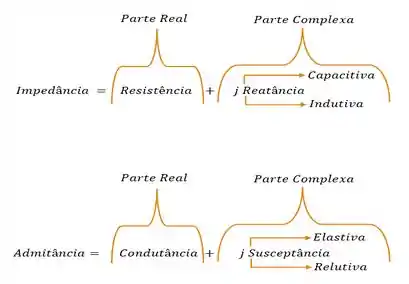
E se vc também estiver se perguntando o por que de nessa questão não haver a parte complexa, é importante ver a definição de Ressonância em   R L C :

“Ressonâcia em R L C   é uma condição onde as reatâncias capacitiva e indutiva são iguais em modúlos, fazendo com que a reatância total seja nula, resultando em uma impedância, puramente resistiva”.

Observe que a reatância será nula, mas a capacitância C e a indutância L não!

Passo 3

Agora vamos encontrar a largura de banda B :

Q = ω 0 B

80 = 200 k r a d s B

B = 2500

Passo 4

Encontrar L   e   C , usando a fórmula geral do passo 1:

Q = R ω 0 L = ω 0 C R = ω 0 B

Para encontrar L :

R ω 0 L = ω 0 B

R L = ( ω 0 ) 2 B

R B ( ω 0 ) 2 = L

40 ⋅ 2500 200 ⋅ 10 3 2 = L

L = 2,5   µ H  

Para encontrar C :

ω 0 C R = ω 0 B

C R =   ω 0 ω 0 B

C = 1 R B

C = 1 40 ⋅ 2500

C = 10 µ F

Passo 5

Por fim, vamos encontrar as frequência de meia potência:

ω 1 ≅   ω 0 - B 2               e               ω 2 ≅   ω 0 + B 2

ω 1 ≅   200 ⋅ 10 3 - 2500 2               e               ω 2 ≅   200 ⋅ 10 3 + 2500 2    

ω 1 ≅   198750 r a d s                   e               ω 2 ≅   201250 r a d s

ω 1 ≅   19,9 M r a d s                   e               ω 2 ≅ 20,1 M r a d s

Resposta

R = 40 Ω

B = 2500

L = 2,5     µ H

C = 10 µ F

ω 1 ≅   19,9 M r a d s                   e               ω 2 ≅ 20,1 M r a d s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine v(t) no Problema 12.26
Os parâmetros do circuito da Figura P12.28 são R = 2,5 kV; L = 50 mH e C = 2 nF. Se Icc = 40 mA, determine i o(t) para t $ 0.
Aplique os teoremas do valor inicial e do valor final a cada par de transformadas do Problema 12.40.
a) Dado que F(s) = l {f (t)}, mostre que - d F(s)/ds = l {t f (t)}. b) Mostre que (-1)^nd^nF(s) ds^n = l{t^nf(t)} . c) Use o resultado de (b) para determinar e l{t^5}, l{tsenbt} e l{te^-tcosh t}.
Os parâmetros do circuito da Figura P12.30 são R = 2 kV; L = 1,6 H e C = 5 mF. Se Vcc for 56 V, determine a) vo(t), para t $ 0. b) i o(t), para t $ 0.