Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 2.2 - Ex. 2

CaIcule v e i .

Passo 1

Falaaaa, galeraaaa! Na figura abaixo temos o circuito que corresponde a essa questão.

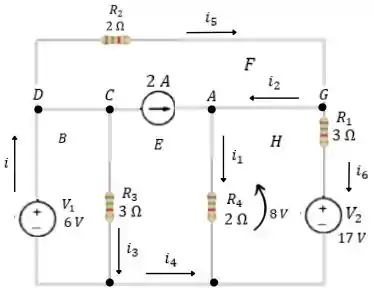
Para resolver essa questão devemos aplicar as Leis de Kirchhoff. Temos:

  • Lei de Kirchhoff das tensões (LKT): “A soma das tensões em torno de uma malha fechada é zero”.
  • Lei de Kirchhoff das correntes (LKC): “A soma de todas as correntes que chegam a um nó do circuito deve ser igual à soma de todas as correntes que deixam esse mesmo nó.”

Passo 2

Bom, primeiro podemos obter o valor da corrente i 1 . Vamos utilizar a seguinte expressão, que é a Lei de Ohm:

V = R ∙ i

Logo,

i 1 = V R = 8 2 = 4   A

Podemos obter a corrente i 2 , aplicando LKC no nó A :

2 + i 2 - 4 = 0

i 2 = 2   A

Passo 3

Aplicando LKT em B :

- 6 + 3 i 3 = 0

i 3 = 2   A

Aplicando LKT em C :

i 4 - 2 - i 3 = 0

i 4 - 2 - 2 = 0

i 4 = 4   A

Aplicando LKT em E :

- 3 i 3 + V 1 + 8 = 0

- 3 2 + V 1 + 8 = 0

V 1 = - 2   V

Aplicando LKT em F :

2 i 5 - V 1 = 0

2 i 5 - - 2 = 0

i 5 = - 2 2 = - 1   A

Aplicando LKC em G :

i 5 - i 2 - i 6 = 0

i 6 = - 3   A

Aplicando LKT em H :

- 8 + 8 i 6 + V = 0

- 8 + 3 - 3 + V = 0

V = 17   V

Aplicando LKC em D :

i - i 5 - i 4 = 0

i - - 1 - 4 = 0

i = 3   A

Prontinho!

Resposta

V = 17   V

i = 3   A

Exercícios de Livros Relacionados

Determine V x no circuito da figura 2.85 .
Para o circuito da figura 2.88 , determine V 0 / V s em termos de α , R 1 , R 2 , R 3 e R 4 . Se R 1 = R 2 = R 3 = R 4 , qual o valor de α que produzirá V 0 V s = 10 ?
Obtenha v 1 a v 3 no circuito da figura 2.81 .
Para o circuito da figura 2.77 , use a LKC para encontrar as correntes nos ramos I 1 a I 4 .
Encontre v 1 e a potência entregue ao resistor de 8 Ω.