Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 23
Calcule para , se
Passo 1
Fala, galerinha. Tudo certinho com vocês?
Já estão craques, tenho certeza disso. Mas, vamos continuar praticando. Olha só esse circuito RL que interessante, tem uma fonte de tensão dependente 😱não precisa se assustar, vamos fazer juntos e arrasar! 💪
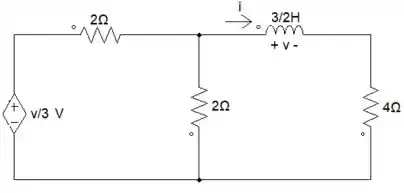
Vamos começar definindo duas correntes em cada malha, vamos denominá-las de . Agora, nós podemos fazer análise de malhas.
Malha 1:
Resolvendo:
Malha 2:
Resolvendo:
Belezinha, pessoal. Agora que já sabemos as equações, vamos pegá-las para formar um sistema de equações e acharmos a EDO do circuito.
Passo 2
Muito bom! Achamos a EDO do circuito, agora vamos achar o Relaxa, é bem facinho 😉
Passo 3
Muito bem! E quanto vale o quando ? Vamos usar a equação . Lembrando que nosso . Vamos lá!
Parecia difícil, mas foi bem de boa né?! 😉