Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 12.Problemas - Ex. 6

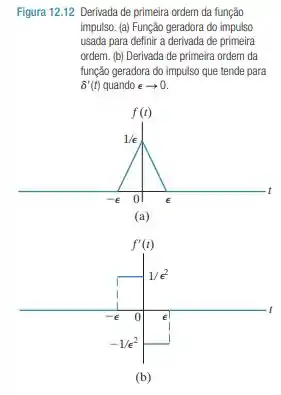
a) Calcule a área sob a função da Figura 12.12(a).

b) Qual é a duração da função quando P = 0?

c) Qual é o valor de f(0) quando ∈   =   0 ?

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre introdução à transformada de Laplace!

  1. Sabemos, analisando a figura trazida no enunciado da questão, que a área citada vai ser a seguinte:

    2. A = 1 2   b h

    Ou seja:

    A = 1 2   2 ∈   q = 1 ∈ = 1

    Passo 2

  2. A duração da função, nesse caso, é zero.
  3. O valor de f, nesse caso, é ∞ .

Resposta

  1. Item a:

    2. A = 1 2   2 ∈   q = 1 ∈ = 1

  2. A duração da função, nesse caso, é zero.
  3. O valor de f, nesse caso, é ∞ .

Então é isso, pessoal! Nos vemos na próxima questão. 😊

Exercícios de Livros Relacionados

A chave no circuito da Figura P13.11 esteve na posição x por um longo tempo. Em t = 0, ela passa instantaneamente para a posição y. a) Construa um circuito no domínio da frequência, para t0. b) Determ
A chave no circuito da Figura P13.15 esteve fechada por um longo tempo antes de abrir em t = 0. a) Construa o circuito no domínio da frequência, para t0. b) Determine I 0 . c) Determine i 0 tp a r at
Um resistor de 200 V está em série com um capacitor de 62,5 mF. Essa combinação em série está em paralelo com um indutor de 400 mH. a) Expresse a impedância equivalente desses ramos paralelos no domín
Não há nenhuma energia armazenada no circuito da Figura P13.20, no instante em que a fonte de tensão é ligada e vg = 325u(t) V. a) Determine Vo e Io. b) Determine vo e i o. c) As soluções para vo e i
Não há nenhuma energia armazenada no circuito da Figura P13.21, no instante em que as fontes são conectadas. a) Determine I 1 seI 2 ( s ) . b) Use os teoremas do valor inicial e final para verificar o