Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.6 - Ex. 4
Calcule para no circuito do Ex. 8.6.2, se as duas chaves são fechadas em e . (Sugestão: Calcule i como antes e observe que é devida às duas fontes.)
Passo 1
Olá amigos, sejam bem-vindos mais uma vez ao RespondeAí. Vamos ajudar vocês nesta questão.
O enunciado da questão já nos forneceu o valor da corrente , isso nos facilita a resolução do problema e devemos analisar o circuito apenas para . O circuito fica da seguinte forma:
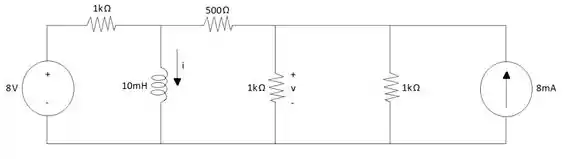
Para encontrar a corrente em devemos considerar as respostas forçada e natural da corrente, sendo assim começaremos pela resposta forçada.
Para a resposta forçada consideramos o circuito em regime permanente e devido ao curto-circuito provocado pelo indutor a aparência do circuito é a seguinte:
Por causa dessa configuração, devemos analisar o circuito como se fossem dois circuitos independentes, um para a fonte de tensão e outro para a fonte de corrente. No final a resposta forçada a soma das correntes que passam pelo mesmo fio.
Passo 2
Para a resposta forçada da fonte de tensão considerando apenas o resistor de 2 Ω teremos a seguinte resposta:
Para a resposta forçada devido à fonte de corrente temos o seguinte:
Assim a resposta forçada fica:
As correntes se somam pois ambas estão entrando no nó:
Passo 3
Agora só falta calcular a resposta natural da corrente, para isso substituímos a fonte de tensão por um fio e a fonte de corrente por um circuito aberto:
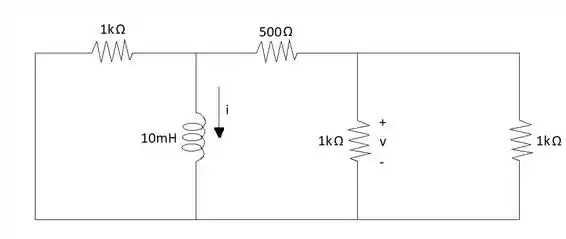
Com esse circuito precisamos calcular a constante de tempo, portanto devemos encontrar a resistência equivalente deste circuito:
Com o valor da constante de tempo podemos escrever a resposta natural da corrente:
Passo 4
Com as duas respostas obtidas basta apenas calcular a constante que aparece na resposta natural usando o valor da resposta forçada e o valor de :
Substituindo na expressão anterior: