Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 56a
(a) Demonstre que para um filtro passa-faixa,
Onde = largura de banda do filtro e é a frequência central
Passo 1
Um filtro passa-faixa deixa passar frequências dentro de uma faixa de frequências e bloqueia ou atenua frequências fora da faixa. Este pose ser construído por meio de um circuito quando o sinal de saída é extraído do resistor,
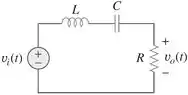
Passo 2
A largura de banda pode ser expressa por
E a frequência de ressonância ou frequência central é dada por
Passo 3
Como a tensão de saída está sobre o resistor e a tensão de entrada é a soma das quedas de tensão, logo a função de transferência pode ser dada por
Passo 4
Organizando o denominador, multiplicando em cima e em baixo por a função de transferência ficará
Passo 5
Para que apareçam os termos que queremos basta dividir o encontrado no passo 4 por
Substituindo o encontrado no passo 2 e arrumando os termos teremos
Exatamente a expressão pedida no enunciado
Resposta
Letra a)