Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 21
Calcule a corrente de linha
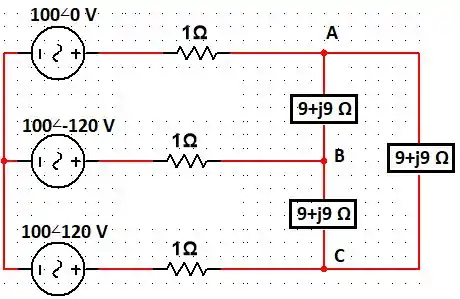
Passo 1
Olha.. de forma limpa, seca e direta pq a gente é brabx haha: o negócio aqui é passar as impedâncias de para e aí, a gente deixa o circuito no formato (pois a corrente de linha é a mesma de fase.. o que vai facilitar demaaaais).
A relação das impedâncias é dada por:
Substituindo valores, temos:
Como as impedâncias são iguais, então:
Passo 2
Assim, como a corrente de fase é igual a corrente de linha para , então:
Em que é a impedância equivalente (a que a gente encontrou somada com o resistor de ). Assim, temos:
Faaacil né?? Responde aí!!!
Resposta
Exercícios de Livros Relacionados
Na Fig. 13.10, a fonte e equilibrada, com sequência de fase positiva, e V e = = 1000V V (eficazes). Calcule Z p , se a fonte entrega 3,6k W com fator de poténcia 0,6 adiantado
Se o fio neutro for removido do sistema do Prob. 13.9, calcule as correntes de linha.
Um sistema equilibrado em Y-Y, trifásico e de sequência de fases positiva, tem V a n = 200 / 0 ∘ V (eficazes) e Z p = 3 + j 4 Ω . As linhas têm uma resistência de 1 Ω cada uma. Calcule a corrente de l
Na Fig. 13.13, a fonte é equilibrada, com sequência de fases positiva, e V a n = 100 ∠ 0 ∘ V (eficazes). Se a impedância de fase é 3 3 ∠ 30 ∘ Ω , calcule a corrente de linha e a potência entregue à ca
Na Fig. 13.13, o sistema de sequência positiva tem V a n = 200 ∠ 0 ∘ V ( eficazes). Calcule Z p , se a fonte entrega 2,4k W , com fator de potência 0,8 atrasado