Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 3

Calcule H s = V 2 ( s ) / V 1 s   e esboce as respostas em amplitude e fase. Mostre que o pico da amplitude e a fase zero ocorrem em ω = 4   r a d / s .

Passo 1

Que que iiiiiissooo!!

Relaxe, relaxe!!

Sabemos que, para uma resistência R , a impedância é:

Z R s = R

E, para uma capacitância C , sua impedância é:

Z C s = 1 s C

Assim, temos o seguinte circuito:

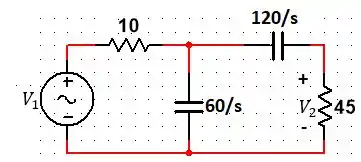
Passo 2

Chamaremos de v a tensão em cima do capacitor de tal forma que:

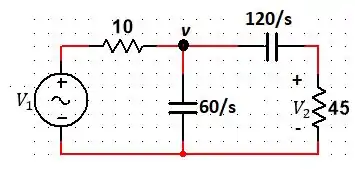
Fazendo o divisor de tensão para ter a relação entre v e V 2 (pq??? Vc vai já entender haha), temos que:

V 2 = v 45 120 s + 45 ∴

v = V 2 45 s + 120 45 s

Passo 3

Fazendo a Lei dos Nós, temos:

V 1 - v 10 = v 60 s + v 120 s + 45 ∴

V 1 10 = v 1 10 + s 60 + s 45 s + 120

Agora sim, vamos substituir o v que tínhamos encontrado antes!! (Não falei que vc ia entende rsrs). Assim, temos:

V 1 10 = V 2 45 s + 120 45 s 1 10 + s 60 + s 45 s + 120 ∴

V 1 10 = V 2 45 s + 120 45 0 s + 45 s 2 + 120 s 60 × 45 s + s 45 s ∴

V 1 = V 2 45 s 2 + 450 s + 720 270 s ∴

V 2 V 1 = 6 s s 2 + 10 s + 16 = H ( s )

Passo 4

Se você observar, verá que H ( s ) tem o seguinte formato:

K s s 2 + B s + ω 0 2

Ou seja, isso nos infere que:

ω 0 2 = 16 ∴

ω 0 = 4   r a d / s

Além disso,

H m á x = K B = 6 10 = 0.6

Resposta

H s = 6 s s 2 + 10 s + 16

Exercícios de Livros Relacionados

Calcule os seguintes números complexos:((5 - j 6) - (2 + j 8))/((- 3 + j 4) (5 - j) + ( 4 - j 6 )) ((240 /_ 75 ° + 160 /_ - 30 °) (60 - j 80))/(( 67 + j 84 ) ( 20 /_ 32 ° )) ((10 + j 20)/(3 + j 4))^2
Determine v ( t ) nas seguintes equações integro-diferenciais usando o método de fasores: v t + ∫ v d t = 10 cos ⁡ t d v d t + 5 v t + 4 ∫ v d t = 20 s e n ( 4 t + 10 ° )
Simplifique o seguinte:f (t) = 5 cos ( 2 t + 15 ° ) - 4 sen ( 2 t - 30 ° ) g (t) = 8 sen t + 4 cos (t + 50 °) h (t) = int_0^t (10 cos (40 t) + 4 sen (40 t)) d t
Uma tensão atermada é dada por v t = 55 cos ⁡ ( 5 t + 45 ° )V . Use fasores para determinar 10 v t + 4 d v d t - 2 ∫ - ∞ t v t d t Suponha que o valor da integral seja zero em t = - ∞ .
Usando fasores, determine:3 cos ( 20 t + 10 ° ) - 5 cos ( 20 t - 30 ° ) 40 s e n (50 t) + 30 c o s ( 50 t - 45 ° ) 20 s e n (400 t) + 10 cos ( 400 t + 60 ° ) - 5 s e n ( 400 t - 20 ° )