Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 19

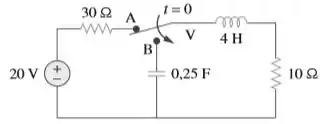
A chave na figura é movida da posição para em (observe que a chave deve ser conectada ao ponto antes de interromper a conexão com . Determine para .

Passo 1

Acho interessante começar esse problema já considerando que a chave já está conectada ao por um tempinho já, então o circuito se resume ah...

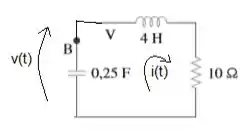
Onde Esse aí é quem devemos encontrar (tensão em cima do capacitor, embora não tenha ficado explicito no enunciado). Bora Resolver esse circuito então?

Passo 2

Bem, esse circuito pode ser resolvido usando a lei das malhas se lembrando de que a tensão em cima do indutor é :

Ainda sabemos que a tensão em cima do capacitor é...

Esse menos é porque a corrente se encontra na mesma direção da tenção, ok? Derivando para tirar essa integral daí...

Por fim, vamos só substituir o ...

Ou seja, as duas equações diferenciais que precisamos resolve são essas aqui:

Passo 3

Beleza, então agora vamos resolvê-las aplicando a transformada de Laplace (nas duas equações)...

Ora, lembrando-se das Laplaces das derivadas...

Perceba então que temos que encontrar essas condições iniciais. Para isso, vamos utilizar aquelas informações lá sobre a chave no tempo !

Passo 4

Bem, no tempo , a chave fecha em , mas ainda não se desconecta de ...

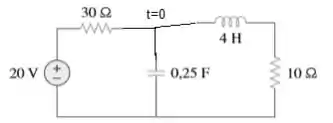
Show, mas antes desse momento, tínhamos uma fonte (de corrente contínua) de , duas resistências e um indutor enquanto que o capacitor estava fora da brincadeira. Ora, em corrente contínua, o indutor é um curto, logo a corrente que circulava não depende dele e sim da fonte e das resistências:

Quando a chave se fechou, a corrente no indutor teve que permanecer a que circulava afinal indutor impede mudanças rápidas na corrente!

Logo...

Agora, para o , tensão inicial sobre o indutor, não foi dito nada no problema sobre e não tem como de calculá-las, logo a gente assume que ele estava descarregado: