Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 50
Calcule a impedância de entrada para o circuito da Figura .
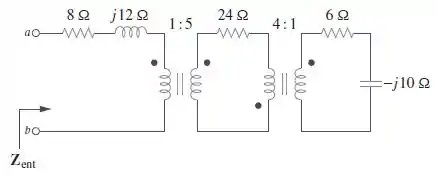
Passo 1
Considere o circuito abaixo. Nós temos dois transformadores ideais no circuito dado. Primeiramente, vamos obter a impedância de entrada . A impedância da carga pode ser referida para o lado primário do transformador usando a seguinte relação:
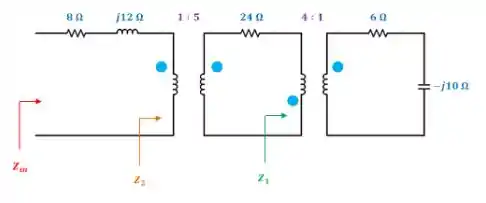
Passo 2
Similarmente ao passo anterior, vamos referir a impedância que está no secundário do segundo transformador para o primário:
Passo 3
Por fim, a impedância de entrada é igual a:
Resposta
A impedância de entrada é igual a:
Exercícios de Livros Relacionados
Considere o transformador trifásico mostrado na Figura 13.136 . O primário é alimentado por uma fonte trifásica com tensão de linha de 2,4k VR M S , enquanto o secundario alimenta uma carga equilibrad
Considere a Figura 13.138 e elabore um problema para ajudar outras estudantes a entender melhor como funciona um transformador trifásico e a conexão estrela-triângulo.
Para atender a uma possível emergência, três transformadores monofásicos de 12470 / 7200 V RMS são conectados em triângulo-estrela para formar um transformador trifásico que é alimentado por uma linha
Um banco de transformadores trifásicos equilibrado com conexão triângulo-estrela representado na Figura 13.137 é usado para abaixar tensões de linha de 4500VR M S para 900VR M S . Se o transformador a
A figura 13.135 ilustra um transformador trifásico que alimenta uma carga ligada em estrela.Identifique a conexão do transformador.Calcule as correntes I 2 e I c Determine a potência média absorvida m