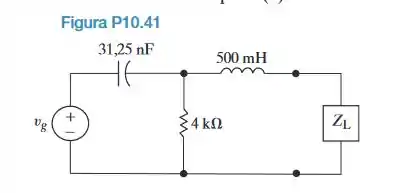
a) Determine a impedância de carga para o circuito da Figura P10.41 para a máxima transferência de potência média à carga, se .

b) Determine a máxima potência média fornecida à carga na parte (a), se .

c) Repita a parte (a), considerando que consista em dois componentes do Apêndice H, cujos valores permitam uma potência média máxima mais próxima do valor calculado na parte (b).

Desativando a fonte de tensão e determinando a impedância de Thevenin em relação aos terminais de carga

Trocando as variáveis por valores

A magnitude da impedância de Thevenin é dada por

Determinando o valor da impedância da carga

Com isso, temos que

Portanto, a resistência de carga que fornece a potência média máxima é .

B - Desconectando a carga e determinando a tensão de Thévenin em relação aos terminais de carga,

Fazendo as substituições, nós temos que

Convertendo para as fasores,

Agora, nós vamos reconectar a impedância de carga calculada ao circuito equivalente de Thevenin, e com isso, determinando a carga da corrente

Fazendo a substituição de valores,

Determinando a magnitude da corrente da carga

O valor da potência média máxima entregue à carga

Fazendo a substituição de valores, nós temos que

Assim, a potência média máxima entregue à carga é

C – Do apêndice H, os valores mais próximos dos resistores são respectivamente, e , da impedância obtida na letra (a), vamos calcular o valor do capacitor

Fazendo a substituição, nós temos que

Portanto,

Do apêndice H, o valor mais próximo é o de 47 , com isso, podemos determinar a impedância

Desde que o resistor de resulta em um perto de do que no caso do resistor , escolhendo . Determinando a corrente de carga

Substituindo os valores,

Convertendo para fasores,

Determine o valor da potência média entregue à carga

Novamente, fazendo a substituição

Com isso, nós temos que

Comparando a potência média calculada com a potência média máxima,

Com isso,

A impedância de carga na qual a potência média está mais próxima do máximo é,