Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.6 - Ex. 3

Calcule a resposta completa i , se i_g = 10 cos 2 t , i (0) = 0 e (d i ( 0^+ ))/(d t) = 8 A // s .

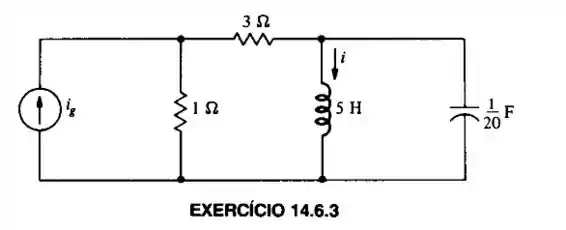
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A primeira que nos ocorre é transformar para o domínio de Laplace e fazer uma análise de malhas, já podemos ver que existirão três malhas, e o circuito no domínio da frequência fica basicamente algo do tipo

Com o valor da fonte sendo igual a

I_g = 10 /_ 0 °

S = 2 j

Logo, temos o seguinte equacionamento para as malhas

{[[I_1 = 10],[(I_2 - I_1) + 3 I_2 + 5 s (I_2 + I_3) = 0],[(20)/(s) I_3 + (I_3 + I_2) 5 s = 0]])

Desenvolvendo um pouco os termos, nós temos que

{[[I_1 = 10],[I_2 (4 + 5 s) + 5 s I_3 = 10],[5 s I_2 + I_3 ((20)/(s) + 5 s) = 0]])

Pegando a última equação, nós podemos fazer o seguinte:

5 s^2 I_2 + I_3 (20 + 5 s^2) = 0 -> I_3 = (- 5 s^2 I_2)/(20 + 5 s^2) = (- s^2 I_2)/(4 + s^2)

Agora, substituindo I_3 na segunda equação, nós obtemos o seguinte resultado

I_2 (4 + 5 s) - (5 s^3 I_2)/(4 + s^2) = 10 -> I_2 = (10 ( 4 + s^2 ))/((4 + 5 s) (4 + s^2) - 5 s^3)

Logo,

I_2 = (10 ( 4 + s^2 ))/(16 + 4 s^2 + 20 s)

Passo 2

Agora vamos saber dos nós do circuito, que vamos chamar de V_a e V_b , com isso, pela análise nodal, nós temos que

10 = V_b + (V_b - V_a)/(3)

Multiplicando todo mundo por 3, nós temos

30 = 3 V_b + V_b - V_a -> V_b = (30 + V_a)/(4)

Com isso, podemos encontrar V_a ,

(((30 + V_a)/(4)) - V_a)/(3) = (V_a)/(5 s) + (5 V_a)/(20)

Desenvolvendo...

(30 - 3 V_a)/(12) = (V_a)/(5 s) + (5 V_a)/(20) -> (10)/(4) - (V_a)/(4) = (V_a)/(5 s) + (5 V_a)/(20)

Um pouco mais rsrs

50 - 5 V_a = (4)/(5) V_a

Com isso, V_a é igual a

V_a = (50)/((4)/(5) + s + 5) = (50 s)/(4 + s^2 + 5 s) , p a r a s = 2 j

Logo, a corrente é igual a

i = (V_a)/(5 s) = (10)/(4 + s^2 + 5 s) = (10)/(5 * 2 j) = - j

Passo 3

A equação característica para a corrente nesse caso é dado por

i (t) = K_1 e^(omega_1 t) + K_2 e^(omega_2 t) + s e n 2 t

Tirando as raízes, nós temos que

4 + s^2 + 5 s = 0

Logo, o delta é igual a

Delta = 25 - 4 * 4

Portanto, omega_1 e omega_2 , é igual a

Delta = (- 5 +- 3)/(2) -> S_1 = - 4 e s_2 = - 1

Resposta

Resposta nos passos

Exercícios de Livros Relacionados

Calcule estes determinantes:|[[10,+,j,6,2,-,j,3],[-,5,-,1,+,j]]| |[[20,/_,-,30,°,-,4,/_,-,10,°],[16,/_,0,°,3,/_,45,°]]| |[[1,-,j,-,j,0],[j,1,-,j],[1,j,1,+,j]]|
Transforme as senoides a seguir em fasores:- 20 cos ( 4 t + 135 ° ) 8 s e n ( 20 t + 30 ° ) 20 cos (2 t) + 15 s e n ( 2 t )
Obtenha as senoides correspondentes a cada um dos seguintes fasores: V 1 = 60 ∠ 15 °V ,ω = 1 V 2 = 6 + j 8V ,ω = 40 I 1 = 2,8 e - j π / 3A ,ω = 377 I 2 = - 0,5 - j 1,2A ,ω = 10 3
Calcule estes determinantes:|[[10,+,j,6,2,-,j,3],[-,5,-,1,+,j]]| |[[20,/_,-,30,°,-,4,/_,-,10,°],[16,/_,0,°,3,/_,45,°]]| |[[1,-,j,-,j,0],[j,1,-,j],[1,j,1,+,j]]|
Simplifique as expressões a seguir:((5 - j 6) - (2 + j 8))/((- 3 + j 4) (5 - j) + ( 4 - j 6 )) ((240 /_ 75 ° + 160 /_ - 30 °) (60 - j 80))/(( 67 + j 84 ) ( 20 /_ 32 ° )) ((10 + j 20)/(3 + j 4))^2 sqrt