Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.Problemas - Ex. 23

Calcule a resposta completa v se v ( 0 ) = 0 . Use as funçőes de rede e superposiçảo

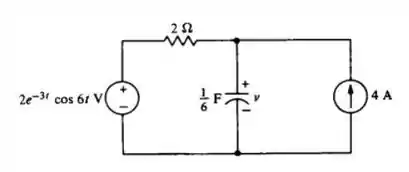
Passo 1

E aí gurizada tudo belezinha? O enunciado pede para a gente determinar a resposta completa v se v ( 0 ) = 0 . Use as funçőes de rede e superposiçảo.

V g = 2 e - 35 c o n ⁡ σ + V

V g ( n ) = 2 < 0 ∘ n = - 3 + 6 y

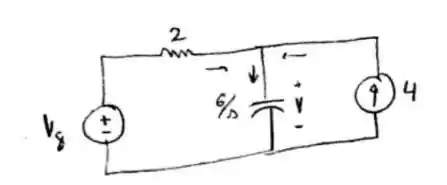
Forte vg

V g - V 2 = s V 6 ⇒ 3 V g - 3 V = s V   ⇒ 3 V g = V ( 3 + p ) ⇒

⇒ V = 3 t 3 + s V g

Passo 2

RN

V n ( t ) = K e - 3 t

RF

V = 3 - 3 + ( - 3 + 6 j ) = 2 = = 1 < - 90 ∘

V f = e - 2 t s e n ⁡ 6 f

Passo 3

Forte 4ª

V c c = 4 ⋅ 2 = 8

V t = K e - 3 t + e - 3 t 67   + 8

CI

V ( 0 ) = 0 ⇒ k + 8 = 0 ⇒ k = - 8 ¨

RT

V ( f ) = 8 + e - 3 t ( - 8 + s e n ⁡ 6 t ) V

Resposta

V ( f ) = 8 + e - 3 t ( - 8 + s e n ⁡ 6 t ) V

Exercícios de Livros Relacionados

Simplifique as expressões a seguir:((5 - j 6) - (2 + j 8))/((- 3 + j 4) (5 - j) + ( 4 - j 6 )) ((240 /_ 75 ° + 160 /_ - 30 °) (60 - j 80))/(( 67 + j 84 ) ( 20 /_ 32 ° )) ((10 + j 20)/(3 + j 4))^2 sqrt
Calcule os seguintes números complexos:((5 - j 6) - (2 + j 8))/((- 3 + j 4) (5 - j) + ( 4 - j 6 )) ((240 /_ 75 ° + 160 /_ - 30 °) (60 - j 80))/(( 67 + j 84 ) ( 20 /_ 32 ° )) ((10 + j 20)/(3 + j 4))^2
Determine v ( t ) nas seguintes equações integro-diferenciais usando o método de fasores: v t + ∫ v d t = 10 cos ⁡ t d v d t + 5 v t + 4 ∫ v d t = 20 s e n ( 4 t + 10 ° )
Simplifique o seguinte:f (t) = 5 cos ( 2 t + 15 ° ) - 4 sen ( 2 t - 30 ° ) g (t) = 8 sen t + 4 cos (t + 50 °) h (t) = int_0^t (10 cos (40 t) + 4 sen (40 t)) d t
Uma tensão atermada é dada por v t = 55 cos ⁡ ( 5 t + 45 ° )V . Use fasores para determinar 10 v t + 4 d v d t - 2 ∫ - ∞ t v t d t Suponha que o valor da integral seja zero em t = - ∞ .