Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.4 - Ex. 2
Calcule a resposta forçada no Ex. 10.4.1, se . (Sugestão: .
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Temos que apenas converter o capacitor, como a frequência já está definida podemos calcular o valor capacitor no domínio da frequência, com isso, nós temos que
Com isso, o circuito fica configurado da seguinte forma
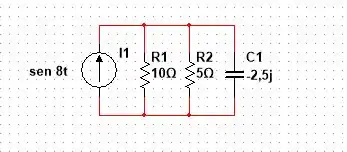
Agora, é somente fazer a análise nodal, já que a tensão é a mesma para todos os pontos, com isso temos o seguinte equacionamento
Fazendo a arrumação dos termos, nós obtemos que
Com isso, nós temos que é igual a
Voltando para o domínio do tempo, nós temos que
Resposta
Exercícios de Livros Relacionados
Mostre, calculando a função de rede H ( s ) = V 2 ( s ) / V 1 ( s ) , que o circuito é um filtro passa-faixa com ω 0 2 = 1 / ( L C ) , B = 1 / C e ganho = 1 . Escolha L e C de forma que B = 0,2eω 1 =
10.21. Para o circuito fasorial mostrado, calcule Zeq e use o resultado para calcular o fasor corrente I. Se w = 2 rad/s, calcule a resposta forçada i correspondente a I.
Mostre que a função de rede V 3 V 1 na figura do Prob. 15.1 é dada por:V 3 V 1 = 1 / L C s 2 + R / L s + ( 1 / L C ) Faça R = 1Ω , L = 1 / 2 H e C = 2F , e mostre que o resultado é um filtro passa-bai
Calcule i ,a corrente em regime permanente, usando fasores