Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 9
Calcule a tensão em regime permanente, usando a análise de laço se e .
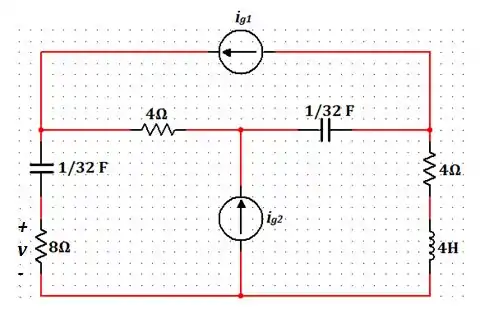
Passo 1
Opaa!! Seguinte... Vamos primeiro passar os valores das fontes para a forma polar e enxergar os capacitores e o indutor em forma de reatâncias.
Lembrando que:
Em que .
Logo, temos:
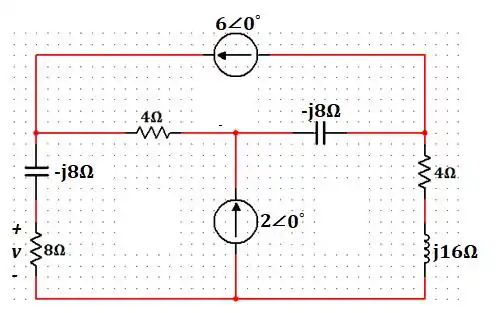
Passo 2
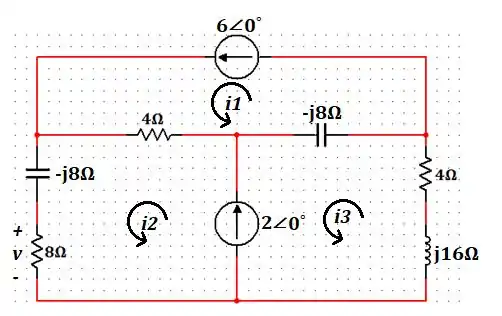Agora, vamos selecionar as seguintes malhas:
Passo 3
Utilizando a Lei dos Kirchhoff das Tensões (LKT) na malha , temos:
Também podemos perceber de cara que as malhas e formam uma supermalha de tal forma que:
Assim, aplicando LKT na supermalha temos:
Sabemos que:
Substituindo o valor de na equação da supermalha, temos:
Passo 4
Assim, a tensão no resistor é dada por:
Resposta
Exercícios de Livros Relacionados
Calcule a tensão v em regime permanente, se v g = 3 cos 2 tV .
Calcule a tensão v em regime permanente.
Calcule a tensão v em regime permanente, se v g = 5 cos 3 tV .
Calcule a corrente i em regime permanente, se v g = 4 cos 3000 tV .
Demonstre (10.59).