Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 26

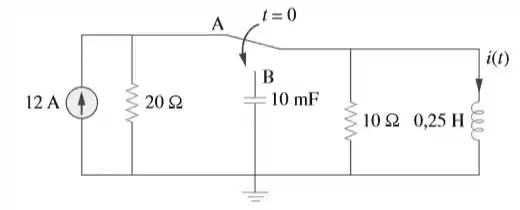
A chave no circuito da figura movida da posição A para B em t = 0 (note que a chave deve ser conectada em B antes de interromper a conexão em A). Determine i ( t ) para t > 0 . Considere também que a tensão inicial no capacitor seja zero.

Passo 1

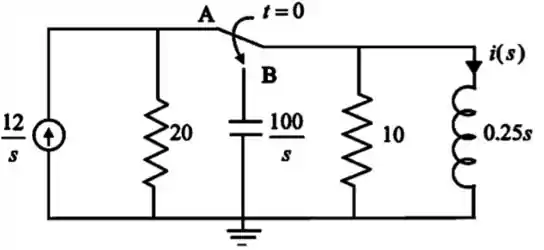
Primeira coisa aqui é passar todos os elementos (ativos e passivos) para o domínio de Laplace (domínio s) e desenhar o circuito novamente.

Fonte de corrente:

12 A ⇒ 12 s

Capacitor:

10 m F   ⇒ 1 s ( 10 m F )

Indutor:

0.25 H   ⇒ s L = 0.25 s

Com essas informações a gente desenha o circuito em Laplace:

Passo 2

Para t < 0 :

Com isso, a gente acha a condição inicial. A corrente no indutor é i ( 0 - ) = 12 A . Como no indutor não pode haver mudança repentina na corrente, então i ( 0 - ) = i ( 0 + ) = 12 A

Passo 3

Para t > 0 :

Vamos colocar uma fonte de corrente inicial paralela ao indutor e a resistência equivalente é mantida

Passo 4

Agora, vamos aplicar as Leis de Kirchhoff no nó V :

V 100 s + V 10 + V 0.25 s + i ( 0 + ) s = 0

V s 100 + V 10 + 4 V s =   - i ( 0 + ) s

V s 2 + 10 s + 400 100 s =   - 12 s

V ( s ) = - 12 s 100 s s 2 + 10 s + 400

V ( s ) = - 1200 s 2 + 10 ( 2 ) 1 2 s + ( 25 - 25 ) + 400

V ( s ) = - 1200 s 2 + 10 s s + 25 + 375

V ( s ) = - 1200 ( s + 5 ) 2 + ( 375 ) 2

Passo 5

Simplificando…

V ( s ) = - 1200 ( s + 5 ) 2 + ( 375 ) 2

V ( s ) = 375 375 - 1200 ( s + 5 ) 2 + ( 375 ) 2

V ( s ) = - 1200 375 375 ( s + 5 ) 2 + ( 375 ) 2

A corrente no indutor é I ( s ) = V ( s ) 0.25 s

I ( s ) = - 1200 375 375 ( s + 5 ) 2 + ( 375 ) 2 0.25 s

I ( s ) = - 247.87 s 375 ( s + 5 ) 2 + ( 375 ) 2

Passo 6

Agora vamos aplicar a transformada de Laplace:

Sabendo que:

s i n ω t ↔ ω s 2 + ω 2

e - a t f ( t ) ↔ F ( s + a )

∫ 0 t f ( t ) ↔ F ( s ) s

Aplicando:

375 ( s + 5 ) 2 + ( 375 ) 2 ↔ e - 5 t s i n ( 375 t )

I ( s ) = - 247.87 s 375 ( s + 5 ) 2 + ( 375 ) 2 ↔ i ( t ) = ( - 247.87 ) ∫ 0 t e - 5 t s i n ( 375 t ) d t

Passo 7

Vamos então achar i ( t )

i ( t ) = ( - 247.87 ) ∫ 0 t e - 5 t s i n ( 375 t ) d t

i ( t ) = ( - 247.87 ) e - 5 t ( - 5 ) 2 + ( 375 ) 2 ( - 5 s i n ( 375 ) - 375 c o s ( - 5 t ) )

i ( t ) = ( - 247.87 ) e - 5 t 25 + 375 ( - 5 s i n ( 375 ) - 375 c o s ( - 5 t ) ) u ( t )

i ( t ) = 0.614675 e - 5 t ( 375 c o s ( 5 t ) + 5 s i n ( 375 t ) ) u ( t )

Então, a corrente i ( t )   ∀   t > 0 é

i ( t ) = 0.614675 e - 5 t ( 375 c o s ( 5 t ) + 5 s i n ( 375 t ) ) u ( t ) m A

Resposta

i ( t ) = 0.614675 e - 5 t ( 375 c o s ( 5 t ) + 5 s i n ( 375 t ) ) u ( t ) m A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na prática, o projeto de filtros R C deve prever a inclusão de resistências de carga e de fote, conforme ilustrado na figura. Seja R = 4k Ω e C = 40n F . Obtenha a frequência de corte quando: R s = 1k
Em um circuito amplificador é preciso um filtro passa-altas R C simples para bloquear a componente C C , enquanto permite a passagem da componente variável com o tempo. Se a frequência de aumento de a
Na prática, o projeto de filtros R C deve prever a inclusão de resistências de carga e de fote, conforme ilustrado na figura. Seja R = 4k Ω e C = 40n F . Obtenha a frequência de corte quando: R s = 0
Em um dispositivo eletrônico é empregado um circuito em série com resistência de 100 Ω , uma reatância capacitiva de 5 k Ω e uma reatância indutiva de 300 Ω , quando usado em 2M H z . Determine a freq
Uma função de transferência é definida apenas quando todas as condições iniciais são zero.(a) verdadeiro (b) falso