Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas Abrangentes - Ex. 102b
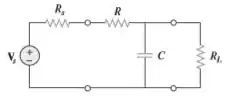
Na prática, o projeto de filtros deve prever a inclusão de resistências de carga e de fote, conforme ilustrado na figura. Seja e . Obtenha a frequência de corte quando:
Passo 1
De acordo com a Teoria, podemos encontrar a frequência de corte através da equação:
Onde é a Resistência equivalente em série com a o capacitor:
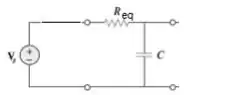
Passo 2
Essa Resistência equivalente, no entanto, pode ser obtida através de Thévenin, no qual devemos obter a resistência equivalente visto pela carga (lembre-se de curto-circuitar a fonte de tensão):
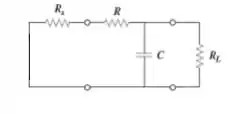
Observe atentamente que do ponto de vista do capacitor a resistência está em paralelo com a Resistência :
Logo...
Passo 3
Pode-se então obter a frequência de ressonância do circuito substituindo-se na equação que vimos:
Resposta
Exercícios de Livros Relacionados
Calcule a frequência de ressonância de cada um dos circuitos da F i g u r a14.82
Considere os circuitos da F i g u r a14.81 e determine a frequência de ressonância ω 0 , o fator de qualidade Q e a largura de banda B .
Calcule a frequência de ressonância de cada um dos circuitos da F i g u r a14.82
Considere o circuito ilustrado na Figura 14.85 e determine:A função de transferência H ω = V 0 ( ω ) / I ( ω ) A amplitude de H em ω 0 = 1r a d / s
Considere o circuito mostrado na Figura 14.84 e determine ω 0 , B e Q visto pela tensão no indutor.