Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas Abrangentes - Ex. 102
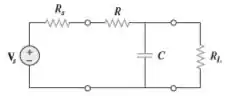
Na prática, o projeto de filtros deve prever a inclusão de resistências de carga e de fote, conforme ilustrado na figura. Seja e . Obtenha a frequência de corte quando:
, .
Passo 1
Ora, se refere a um curto, enquanto que significa um circuito aberto na prática:
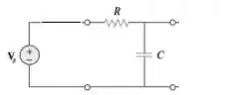
Logo, trata-se de um circuito série normal e para encontrar a frequência de ressonância , basta seguirmos a Teoria:
Passo 2
Substituindo-se os valores dados no enunciado...
Resposta
Exercícios de Livros Relacionados
Determine que tipo de filtro é aquele da Figura 14.87 . Calcule a frequência de corte f c .
Elabore um problema para ajudar outros estudantes a entender melhor os filtros passa-altas passivo.
Projete um filtro passa-baixas R L que usa uma bobina de 40m H e tem frequência de corte 5k H z .
Projete um filtro passa-faixa tipo R L C em série com frequências de corte 10k H z e 11k H z . Considerando C=80p F , determine R , L e Q .
Projete um filtro rejeita-faixa passivo com ω 0 =10r a d / s e Q=20 .