Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 46

A chave no circuito da Figura P7.46 esteve aberta por um longo tempo, antes de fechar em t = 0. Determine vo (t) para t $ 0+.

Passo 1

Para t < 0 :

i 45 m H = 80 2000 V Ω = 40   m A

Passo 2

Para t > 0 : Depois de fazer o equivalente de Thévenin do circuito, temos a seguinte a configuração do circuito:

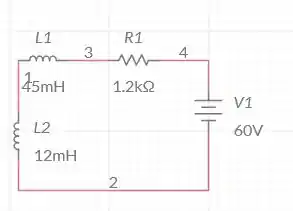
Com isso, utilizando a equação geral para a corrente, obtemos a seguinte configuração:

i = V s R + I 0 - V s R e - t τ

Para o cálculo da inversa da constante de tempo (até para ser um pouco mais direto), só precisa inverter os termos entre o resistor e a indutância equivalente.

1 τ = R L = 1200 60 × 10 - 3 = 20000

Lembra que a corrente no indutor de 45   m H é igual a 40   m A ? Então ela será a nossa corrente inicial, logo:

I 0 = 40   m A

Com isso, é possível calcular também a corrente “final”, que é dada depois de um período muito, muito, muito longo, na qual o circuito se estabiliza.

I f = V s R = 60 1200 = 50   m A

Logo, com isso, temos i :

i = 0,05 + 0,04 - 0,05 e - 20000 t = 50 - 10 e - 20000 t   m A ,     t ≥ 0

E o v 0 usa a fórmula v = L d i d t para encontrar o valor:

v 0 = 0,045 d i d t = 0,045 - 0,01 - 20000 e - 20000 t = 9 e - 20000 t   V ,     t ≥ 0 +

Resposta

v 0 = 9 e - 20000 t   V ,     t ≥ 0 +

Exercícios de Livros Relacionados

A chave mostrada na Figura P7.9 esteve aberta durante um longo tempo, antes de seu fechamento em t = 0 .a) Determine i 0 0 - , i L 0 - e v L 0 - .b) Determine i 0 0 + , i L 0 + e v L 0 + .c) Determine
A chave no circuito da Figura P7.8 esteve fechada por um longo tempo, antes de ser aberta em t = 0 .a) Determine i 1 0 - e i 2 0 - .b) Determine i 1 0 + e i 2 0 + .c) Determine i 1 t para t ≥ 0 .d) De
[a] - Deduza as expressões para as correntes i1(t) e i2(t) para t ≥ 0 . [b] - Use as expressões deduzidas em (a) para determinar i1( ∞ ) e i2( ∞ ).
Relacionada a questão 47. a) a energia total dissipada no resistor de 40 V;b) a energia retida nos indutores; c) a energia inicial armazenada nos indutoresQuestão bem direta, vamos resolver!!
[a] - Determine v 0 t em função de I g , R1, R2 e L.[b] - Explique o que acontece com v 0 ( t ) quando R2 aumenta indefinidamente.[c] - Determine v S W em função de I g , R1, R2 e L.[d] - Explique o q