Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 4
Se o circuito está em regime permanente em , calcule para .
Passo 1
Iae, meus queridos! Td blzinha?
Adianto que essa questão vai ser tranquila, só pra relaxar.
Primeiro de tudo, temos que ir em busca do do capacitor.
Em regime permanente em , podemos considerar o circuito da seguinte forma:
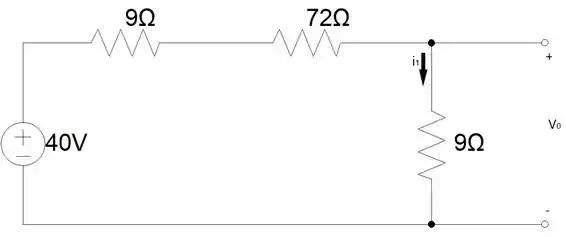
A tensão no resistor paralelo ao capacitor, vai ser nosso e pelo circuito estar em regime permanente, podemos considerar o capacitor como um circuito aberto.
Aplicando a lei de Ohm na malha para encontrar :
Calculando :
Passo 2
Para , podemos considerar o circuito RC:
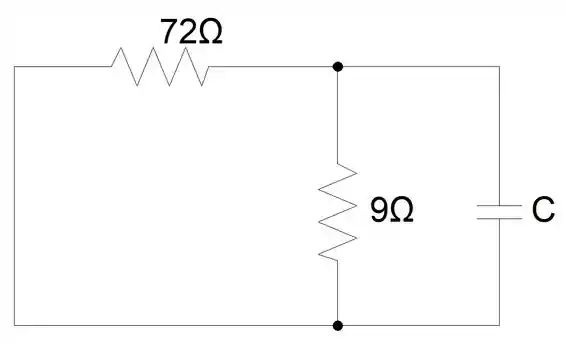
Nos resta apenas calcular desse circuito, e substituir os valores na equação geral .
A questão nos deu o valor de , assim, calculamos .
Substituindo os valores encontrados na equação geral .
Foi de boa, né? Bora pra próxima.