Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 46
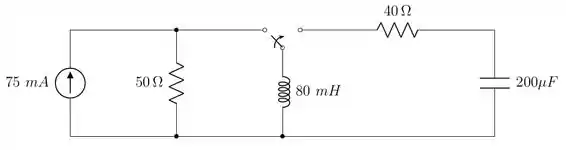
A chave no circuito da Figura P8.46 esteve na posição por um longo tempo. Em , ela passa instantaneamente para a posição . Determine para .
Passo 1
Faaaaaaaaaaaaala, pessoal! Vamos dar continuidade na resolução de circuitos chaveados. Como é de praxe, o que temos que fazer é calcular a tensão no capacitor e a corrente no indutor antes do chaveamento. É possível perceber que na situação mostrada antes do chaveamento não há nenhuma fonte de tensão na malha do capacitor, logo
Para encontrarmos a corrente no indutor, vamos olhar para a figura abaixo:
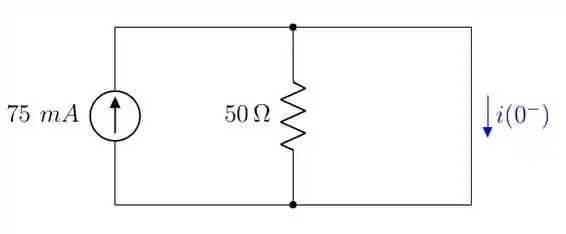
Observe que o resistor de fica curto-circuitado, fazendo com que a corrente que circule no indutor seja toda a corrente da fonte. Logo
Passo 2
Para analisarmos a situação posterior ao chaveamento, temos que calcular as frequências e :
e
Como , temos que a resposta do circuito é criticamente amortecida e a sua forma é do tipo
Passo 3
Escolhendo , vamos obter
Lembrando que o “A” que acompanha o se refere à unidade de corrente, ampère, e não a constante. #FicaADica
Outra expressão é a derivada da corrente. Ela irá aparecer quando derivarmos a tensão no capacitor. Assim,
Derivando a corrente, temos
Escolhendo , vamos obter
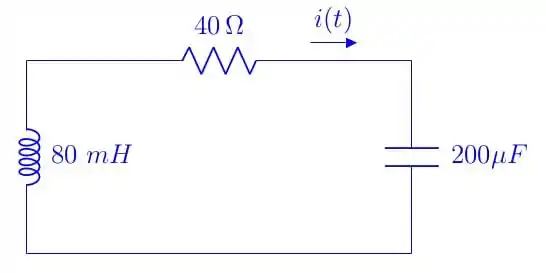
Para encontrarmos o valor de precisamos fazer a LKT para o circuito depois do chaveamento. Vamos colocá-lo aí para conseguirmos visualizar de forma fácil a equação que queremos:
Passo 4
De posse do circuito, fica fácil fazer a LKT:
Como
Além disso,
temos então que
Com isso, podemos escrever como sendo
E assim, finalizamos mais uma questão. Vamos embora que a próxima questão tomou uma radiação de raios gama e está gigante.