Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 47

A chave do circuito mostrado na Figura P8.47 esteve fechada por um longo tempo. Ela se abre em t = 0 . Determine v 0 ( t ) para t ≥ 0 + .

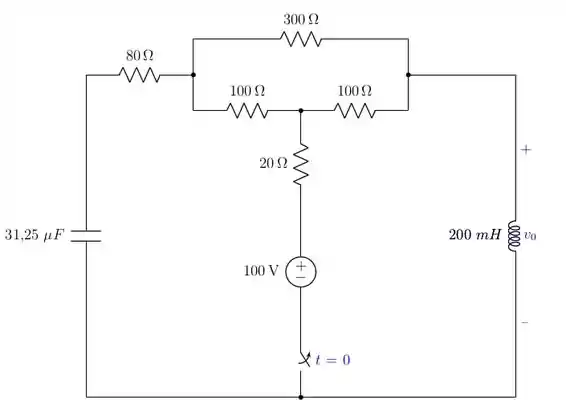
Passo 1

Salve, salve, família. Aqui estamos nós para mais um circuito, só que agora temos uma configuração um pouco mais “parruda”. Não tem problema, vamos resolver como sempre fazemos.

Como se trata de um circuito chaveado, temos que estudar seu comportamento antes e depois do chaveamento

Para t < 0 , a chave ficou fechada durante muito tempo, logo o capacitor se comporta como um circuito aberto e o indutor como um curto circuito. Assim:

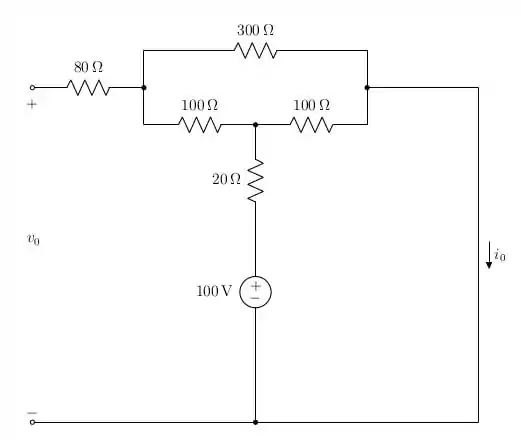
Perceba que nesta figura o resistor de 80   Ω está “sobrando”, é o “vupa”, tá “segurando vela”. Então ele pode ser descartado de nossa análise. Além disso, temos 2 malhas por onde circula corrente. Vamos chamar a corrente que circula na malha de baixo de i 0 para combinar com a corrente no indutor em t = 0 - . Com isso, chamamos a corrente na malha de cima de i 1 , tudo bem?

Vamos então para as equações:

100 = 20 ⋅ i 0 + 100 i 0 - i 1 ⇒ 120 i 0 - 10 0 i 1 = 100 ∴ 6 i 0 - 5 i 1 = 5

A segunda malha nos dá a seguinte equação:

300 + 100 i 1 + 100 i 1 - i 0 = 0 ⇒ - 100 i 0 + 500 i 1 = 0 ⇒ - i 1 + 5 i 2 = 0

Juntando essas duas equações num sistema, vamos obter

6 i 0 - 5 i 1 = 5 - i 1 + 5 i 2 = 0

Resolvendo esse sistema, obtemos

i 0 = 1   A                                 e                             i 1 = 0,2   A

A informação das correntes será útil para encontrarmos v 0 pela LKT (Lembrando que o resistor de 80   Ω continua segurando vela, ou seja, ele não entra nesta conta:

v 0 = - 100 i 1 - 20 i 0 + 100 = - 100 ⋅ 0,2 - 20 ⋅ 1 + 100

v 0 = 60   V

Como o valor foi positivo, a polaridade que escolhemos está correta.

Passo 2

Quando t > 0 , a chave abre e o ramo que contém a fonte de tensão e o resistor de 20   Ω são desconectados e o circuito resultante é

A associação em paralelo nos fornece

R e q 1 = 300 ⋅ 200 300 + 200 = 60000 500 ⇒ R e q 1 = 120   Ω

Juntando essa resistência equivalente à resistência de 80   Ω em série com o capacitor, vamos obter uma resistência de 100   Ω e o circuito simplificado fica

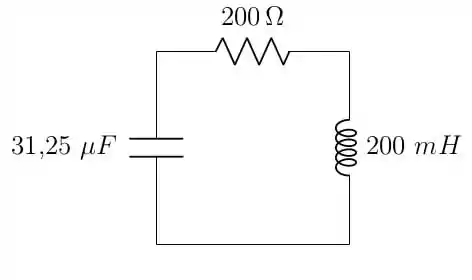
Perceba que reduzimos o circuito inicial a esse circuito RLC série beeeeeeeem mais simples. Agora vamos calcular as frequências para saber o tipo de resposta:

α = R 2 L = 200 2 ⋅ 0,2 ⇒ α = 500 r a d s

e

ω 0 2 = 1 L C = 1 0,2 × 31,25 ⋅ 10 - 6 ⇒ ω 0 2 = 160000 r a d 2 s 2 ⇒ ω 0 = 400 r a d s

Como α 2 > ω 0 2 , então a resposta é superamortecida e é do tipo

i 0 t = A 1 e s 1 t + A 2 e s 2 t

vamos precisar calcular as raízes da equação característica:

s 1,2 = - α ± α 2 - ω 0 2 = - 500 ± 500 2 - 400 2 = - 500 ± 300   r a d / s

⇒ s 1 = - 200 r a d s                        e                       s 2 = - 800 r a d s

Assim,

i 0 t = A 1 e - 200 t + A 2 e - 800 t

Passo 3

Para encontrarmos os valores de A 1 e A 2 vamos começar escolhendo t = 0 na equação da corrente:

i 0 0 = A 1 e - 200 × 0 + A 2 e - 800 × 0 ⇒ 1 = A 1 + A 2

Vamos agora derivar a expressão da corrente:

d i 0 d t = A 1 - 200 e - 200 t + A 2 - 800 e - 800 t

⇒ d i 0 d t = - 200 A 1 e - 200 t - 800 A 2 e - 800 t

Falta agora encontrarmos o valor de d i 0 / d t e isso será feito usando a definição da equação da tensão no indutor e a LKT:

v L - v C + v 200 Ω = 0 ⇒ L d i 0 0 d t = 60 - 200 ⋅ 1 = - 140 0,2 ⇒ d i 0 0 d t = - 700 A s

Se este passo ficou confuso, lembre-se que a corrente i 0 circula pelo indutor de cima para baixo, o que faz com que ela tenha o sentido horário no circuito reduzido. Além disso, encontramos no começo de nossa análise para t < 0 que a polaridade da tensão no capacitor era positiva na parte de cima, por isso os sinais na equação estão do jeito que estão.

Fazendo t = 0 na equação da derivada da corrente, obtemos

d i 0 0 d t = - 200 A 1 e - 200 × 0 - 800 A 2 e - 800 × 0 ⇒ - 700 = 200 A 1 - 800 A 2

Assim, o nosso sistema será

A 1 + A 2 = 1 - 2 A 1 - 8 A 2 = - 7

Resolvendo esse sistema, obtemos

A 1 = 166,7   m A                       e                       A 2 = 833,3   m A

Com isso, a corrente no indutor será dada por

i 0 t = 166,7 e - 200 t + 833,3 e - 800 t   m A ,     t ≥ 0  

Passo 4

Agora que chegamos até aqui, tudo o que temos que fazer é aplicar novamente a equação da tensão no indutor:

v L = L d i d t ⇒ v 0 = 0,2   - 200 ⋅ 0,167 ⋅ e - 200 t - 800 ⋅ 0,83 ⋅ e - 800 t

∴ v 0 t = - 6,67 e - 200 t - 133,33 e - 800 t   V   ,     t ≥ 0  

E assim finalizamos mais uma questão. Let’s Bora pra próxima!

Resposta

v 0 t = - 6,67 e - 200 t - 133,33 e - 800 t   V   ,     t ≥ 0

Exercícios de Livros Relacionados

Um circuito RLC em série possui os seguintes parâmetros: R = 1k Ω ,L = 1 HeC = 10n F . Que tipo de amortecimento é apresentado pelo circuito?
A chave da Figura 8.91 é aberta em t = 0 após o circuito ter atingido o estado estável. Determine R e C de modo que α = 8N p / s e ω d = 30r a d / s .
Dado o circuito da Figura 8.90 , determine v ( t ) para t0 .
Determine v ( t ) para t0 no circuito da Figura 8.87 .
A chave no circuito da Figura 8.88 é deslocada da posição a para a posição b em t = 0 . Determine i ( t ) para t0 .