Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 50

50-

O resistor do circuito mostrado na Figura P8.49 é trocado por um de 250 Ω. A energia inicial armazenada ainda é igual a zero. Determine vo(t) para t ≥ 0.

Passo 1

Então, vamos a luta. Essa questão é tranquila, basta que a gente pense um pouquinho, vamos nessa companheiro?!

A questão diz que o resistor mostrado na Figura P8.49 é trocado por um de 250 Ω. Logo, a gente vai usar o circuito como base, mas nos cálculos a gente substitui os valores, partiu?!

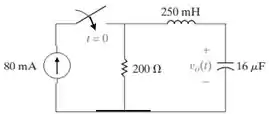
Figura P8.49

Passo 2

Dando sequencia a nossa resolução, temos:

α   = R 2 L   = 250 2 0 , 025   =   500 r a d / s  

ω o   = 1 L C   =   1 ( 250   ×   10   - 3 ) ( 16   ×   10 - 6 )   =   500 r a d / s  

α     2 =   ω     0 2   ,   c r i t i c a m e n t e   a m o r t e c i d o  

v o   =   V f   +   D ' 1   t e - 500 t   +   D '   2 e   - 500 t  

v o 0 =   0   =   V f   +   D ' 2   v o ∞ =   250 0 , 08 =   20 V

D '   2   =   - 20 V  

Passo 3

Para fechar com chave de ouro:

d v o d t (0) = 0 = D ' 1 - α D ' 2 , portanto

D ' 1 = (500)*(-20) = -10000 V/s

vo(t) = 20 - 10000t e - 500 t - 20 e   - 500 t V, t ≥ 0

Resposta

vo(t) = 20 - 10000t e - 500 t - 20 e   - 500 t V, t ≥ 0

Exercícios de Livros Relacionados

Para o circuito da Figura 8.97 , determine i ( t ) para t0 .
Determine a tensão de saída v 0 ( t ) no circuito da Figura 8.94 .
Usando a Figura 8.9 3 , elabore um problema para ajudar outros estudantes a entenderem melhor a resposta a um degrau de um circuito R L C em paralelo.
Determine i ( t ) para t0 no circuito da Figura 8.96 .
Dado o circuito da Figura 8.95 , determine i ( t ) e v ( t ) para t0 .