Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 64
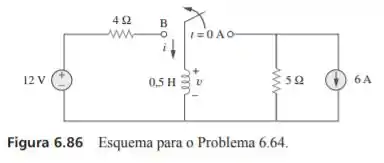
A chave na figura 6.86 se encontra na posição há muito tempo. Em , a chave passa da posição para e é do tipo abre-fecha, de modo que não haja interrupção na corrente do indutor. Determine:
para .
logo após a chave ter passa para a posição .
bem depois de a chave já estar na posição .
Passo 1
Quando a chave se encontra na posição temos , agora quando a chave se encontra na posição temos . Além disso temos . Portanto,
Passo 2
Após a chave ter passado para a posição vamos ter a seguinte configuração
Depois de a chave permanecer no estado nós vamos ter o estado estacionário em que o indutor se torna um curto-circuito para que possamos ter.
Resposta
Exercícios de Livros Relacionados
A tensão nos terminais do indutor de 750 mH da Figura P6.7(a) é mostrada na Figura P6.7(b). Sabe-se que a corrente i do indutor é igual a zero para t ≤0 . a) Escreva as expressões para i em t ≥ 0 . b)
Avalie a integral ∫ 0 ∞ pd t para o Exemplo 6.2. Comente o significado do resultado.
Sabe-se que a corrente em um indutor de 50m Hé é i=120m A ,t ≤0 ; i=A 1 e - 500 t+A 2 e - 2.000 tA ,t ≥0 A tensão no indutor (convenção passiva) é 3 V em t = 0. a) Determine a expressão para a tensão
Sabe-se que a corrente em um indutor de 150 mH é i L=25 t e - 500 tAp a r at≥ 0 Determine a tensão no indutor para t0 (Suponha a convenção passiva)Determine a potência (em microwatts) nos terminais do
O pulso triangular de corrente mostrado na Figura P6.2 é aplicado a um indutor de 500 mH. a) Escreva as expressões que descrevem i(t) nos quatro i n t e r v a l o st,0 ,0 ≤t-25m s ,25m s ≤t ≤50m set.5