Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 38

As chaves 1 e 2 no circuito da Figura P8.38 são sincronizadas. Quando a chave 1 abre, a chave 2 fecha e vice-versa. A chave 1 esteve aberta por um longo tempo antes de fechar em t = 0 . Determine i L ( t ) para t ≥ 0 .

Passo 1

Show de bola, pessoal! Vamos começar a luta contra esse mostro usando a técnica “dividir para conquistar”, ou seja, vamos dividi-lo em partes pequenas, fazer nossas análises e obter os dados mais importantes para nós.

Sabemos que as informações iniciais são a tensão no capacitor e a corrente no indutor, sendo assim, vamos começar por eles:

Quando a chave 1 está aberta, as duas malhas da esquerda estão isoladas:

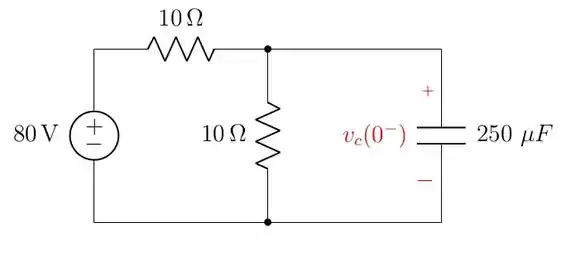
Sendo assim, v c 0 - pode ser obtido por um simples divisor de tensão. Como as duas resistências são iguais, a tensão da fonte se divide igualmente. Assim:

v c 0 - = 40   V

Para analisarmos a corrente no indutor antes do fechamento da chave, teremos que considerar o indutor como um curto-circuito. Isto está representado na figura abaixo:

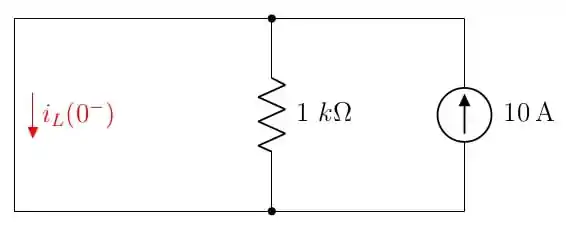
Assim, a corrente no indutor tem o mesmo valor da corrente na fonte, logo:

i L 0 - = 10   A

Além disso, haverá na resposta final um termo relativo à resposta forçada. Assim, temos que calcular i L ( ∞ ) . Nessa situação, com as chaves nos estados devidos, o circuito será o que é representado abaixo:

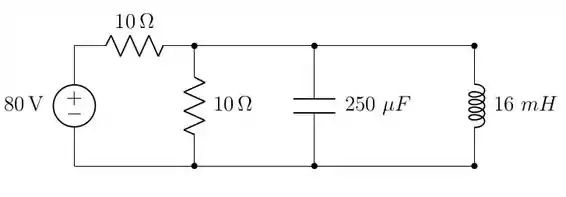Nessa situação, de regime permanente, o capacitor funciona como um circuito aberto e o indutor como um curto circuito. Assim, a representação seria

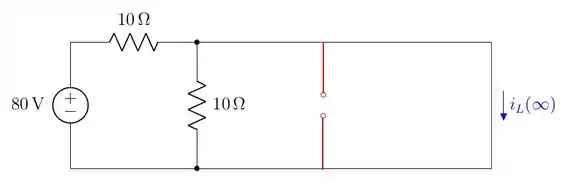
Essa configuração curto-circuita o resistor de 10   Ω que está na vertical. Assim, a única corrente que circula é a corrente no resistor de 10   Ω ligado à fonte. Logo

i L ∞ = 80 10 ∴ i L ∞ = 8   A

Passo 2

Uma vez que obtivemos os valores associados às condições inicial e final, vamos achar os componentes α e ω 0 para conhecermos a forma da resposta da corrente:

α = 1 2 ⋅ R ⋅ C = 1 2 ⋅ 5 ⋅ 250 ⋅ 10 - 6 ∴ α = 400   r a d / s

ω 0 = 1 L ⋅ C = 1 16 ⋅ 10 - 3 ⋅ 250 ⋅ 10 - 6 ∴ ω 0 = 500   r a d / s

Desses dois valores, temos que α 2 = 160.000 < ω o 2 = 250.000 . Logo, a resposta do circuito é subamortecida e usaremos a equação 8.61 para escrevermos a resposta. Mas não se preocupe que eu não farei você voltar as páginas para procurar. Eu coloco aqui pra te poupar tempo, neném!

i L t = i L ∞ + B 1 e - α t cos ⁡ ω d t + B 2 e - α t sin ⁡ ω d t

Aqui cabe uma observação que é a seguinte. Foi acrescentado o termo i L ∞ porque o circuito tem uma fonte de tensão que produzirá a resposta forçada, por isso deve ser incluído na equação o termo correspondente a essa resposta.

Passo 3

Seguimos nosso caminho calculando o valor de ω d :

ω d = ω 0 - α = 500 2 - 400 2 ∴ ω d = 300   r a d / s

Juntando tudo o que temos até agora e colocando na equação final, obtemos:

i L t = 8 + B 1 e - 400 t cos ⁡ 300 t + B 2 e - 400 t sin ⁡ 300 t

Usando a equação em t = 0 , obtemos:

i L 0 = 8 + B 1 e - 400 ⋅ 0 cos ⁡ 300 ⋅ 0 + B 2 e - 400 ⋅ 0 sin ⁡ 300 ⋅ 0

i L 0 = 8 + B 1 ⇒ 10 = 8 + B 1 ⇒ B 1 = 10   A

No entanto, não conhecemos outro valor de corrente, fora que teríamos uma expressão bem complicada para resolver, caso quiséssemos trabalhar com esse valor. Então, como proceder?

Trabalhar com a equação final se torna inviável, mas E SE derivarmos a equação, o que obteríamos? Vamos fazer um teste. Começamos reescrevendo a equação com o que temos até agora:

i L t = 8 + 2 e - 400 t cos ⁡ 300 t + B 2 e - 400 t sin ⁡ 300 t

Assim

d i L t d t = 0 + 2 - 400 e - 400 t cos ⁡ 300 t + e - 400 t ⋅ 300 ⋅ sin ⁡ 300 t + B 2 [ - 400 e - 400 t sin ⁡ 300 t + e - 400 t ⋅ 300 ⋅ cos ⁡ 300 t

Em t = 0 , obtemos o seguinte resultado:

d i L 0 d t = - 2 ⋅ 400 + 300 ⋅ B 2

Além disso, temos que d i L ( 0 ) / d t     =   V 0 / L , logo

- 800 + 300 B 2 = 40 0,016 = 2500 ⇒ B 2 = 11   A

Passo 4

Juntando tudo o que temos, vamos chegar na resposta final:

i L t = 8 + 2 e - 400 t cos ⁡ 300 t + 11 e - 400 t sin ⁡ 300 t   A ,     t ≥ 0

Resposta

i L t = 8 + 2 e - 400 t cos ⁡ 300 t + 11 e - 400 t sin ⁡ 300 t   A ,     t ≥ 0

Exercícios de Livros Relacionados

Para o circuito da Figura 8.65, determine:(a) v 0 +ei ( 0 + ) (b) d v ( 0 + ) / d ted i ( 0 + ) / d t (c) v ∞ei ( ∞ )
Considere a Figura 8.63 e elabore um problema para ajudar outros estudantes a entenderem melhor como determinar os valores inicial e final.
Para o circuito da Figura abaixo, determine:(a) i L ( 0 + ) , v c ( 0 + ) e v R ( 0 + ) (b) d i L ( 0 + ) / d t , d v C ( 0 + ) / d t e d v R ( 0 + ) / d t (c) i L ( ∞ ) e v C ( ∞ ) e v R ( ∞ ) .
No circuito da Figura 8.67, determine:(a) v R 0 +ev L ( 0 + ) (b) d v R ( 0 + ) / d ted v L ( 0 + ) / d t (c) v R ∞ev L ( ∞ )
A resposta a um degrau de um circuito R L C é descrita por d 2 i d t 2 + 2 d i d t + 5 i = 10 Dado que i 0 = 2 e d i 0 d t = 4 , determine i ( t ) .