Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 3
Para o circuito da Figura abaixo, determine:
(a) , e
(b) , e
(c) ) e e .
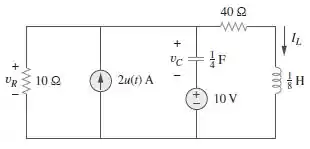
Passo 1
Primeiro vamos analisar o circuito antes da chave abrir, ou seja, . Sabemos que, u(t) = 0.
Note que, o capacitor pode ser tratado como um circuito aberto, e o indutor como um curto-circuito. Assim, o circuito equivalente é,
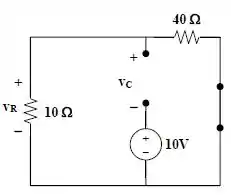
Observe que,
Mas se fizermos LKV, obtemos:
Passo 2
Para , o indutor não pode sofrer uma variação abrupta de corrente e o capacitor de tensão, portanto
Note que, a tensão do capacitor anula com a tensão da fonte, portanto a corrente de 2 A flui toda para o capacitor, logo,
Passo 3
Para o item b) temos,
Como,
Portanto,
Passo 4
Similarmente, temos
Como,
Substituindo,
Note que,
Se derivarmos, obtemos:
Passo 5
Note que o circuito tem uma alimentação, então se substituirmos o capacitor por um circuito aberto e um indutor por um circuito fechado, obtemos:
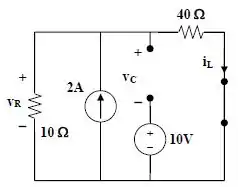
Se resolver o circuito teremos:
Por divisor de corrente,
() = 10(2)/(40 + 10) = 400 mA
Por LKV,
() = 2[10||40] –10 = 16 – 10 = 6V
() = 2[10||40] = 16 V
Resposta
c) () = 10(2)/(40 + 10) = 400 mA
() = 2[10||40] –10 = 16 – 10 = 6V
() = 2[10||40] = 16 V