Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 46
Para o circuito na Figura 7.113, Determine
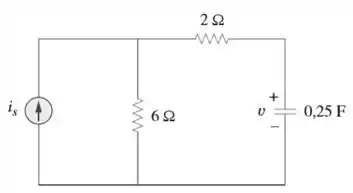
Passo 1
Okay galera, essa questão tem um circuito bem básico, então vai ser bastante simples a resolução! Primeiro, vamos definir o nosso Tau, essencial para a formula do estado estacionário!
Passo 2
Aí ficou fácil, só jogar na fórmula!
Resposta
Exercícios de Livros Relacionados
O circuito R C na figura é usado para um compensador de avanço em um projeto de um sistema. Obtenha a função de transferência do circuito.
Em determinada aplicação, um filtro passa-baixas R C simples é projetado para reduzir o ruído de alta frequência. Se a frequência de corte desejada for 20k H z e C = 0,5μ F , determine o valor de R .
Na prática, o projeto de filtros R C deve prever a inclusão de resistências de carga e de fote, conforme ilustrado na figura. Seja R = 4k Ω e C = 40n F . Obtenha a frequência de corte quando: R s = 1k
Em um circuito amplificador é preciso um filtro passa-altas R C simples para bloquear a componente C C , enquanto permite a passagem da componente variável com o tempo. Se a frequência de aumento de a
Na prática, o projeto de filtros R C deve prever a inclusão de resistências de carga e de fote, conforme ilustrado na figura. Seja R = 4k Ω e C = 40n F . Obtenha a frequência de corte quando: R s = 0