Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas Abrangentes - Ex. 103
O circuito na figura é usado para um compensador de avanço em um projeto de um sistema. Obtenha a função de transferência do circuito.
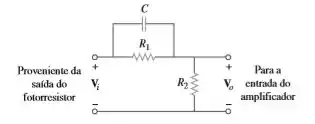
Passo 1
Podemos encontrar a função de transferência através da razão entre a tensão de saída pela tensão de entrada:
Para obter tal relação, encontrar qual é essa impedância que estou chamando de
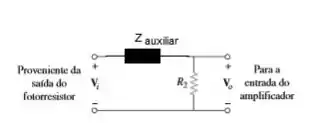
E depois fazer o divisor de tensão! Bora?
Passo 2
A gente pode encontrar essa Impedância, fazendo o paralelo entre a impedância capacitiva e o resistor:
Onde você tem que se recordar que a impedância capacitiva é calculada através da Capacitância: . Show! Então, através do paralelo...
Fazendo agora o divisor de tensão para tirar em função de ...
Ora! é a função de transferência pedida! Substituindo o ...
Se você em uma prova não tem mais tempo, pode parar aí em cima, pois a função de transferência é essa. Mas se você tem ainda um tempinho é bom simplificar essa fração horrorosa:
Tirando o dessa primeira fração...
Tirando da Segunda...
Então, concluímos que a função de transferência em uma forma muito mais agradável é: