Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 61

No circuito da Figura 7.126, i s varia de 5 A para 10 A em t = 0; isto é, i s = 5u(–t) + 10u(t). Determine v e i.

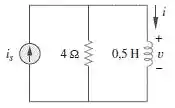
Passo 1

Primeiro vamos transformar essa fonte de corrente para uma fonte de tensão. Temos que,

V = R * I

v s = 4 * 5 u - t + 10 u t  

v s = 20 u - t + 40 u t

O circuito equivalente é dado abaixo:

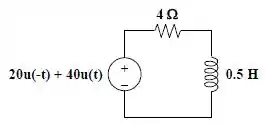
Passo 2

Note que, esse circuito é um RL série. Portanto a constante de tempo é dada por:

τ = L R = 1 / 2 4 = 1 8

Lembre-se que, a equação que descreve a corrente em função do tempo para esse circuito é dada por:

i t = i ∞ + i 0 - i ∞ e - t / τ

Para t=0:

Observe que, para t=0, a fonte tensão fornece 20V, e como é constante podemos substituir o indutor por um curto. Assim,

i 0 = 20 V 4 Ω   = 5 A

Para t = ∞ :

Quando o tempo tende ao infinito a tensão é constante em 40V. Desse modo podemos substituir o indutor por um curto novamente. Assim,

i ∞ = 40 V 4 Ω = 10 A

Portanto a equação para a corrente é dada por:

i t = 10 - 5 e - 8 t u t   A

Passo 3

Como já obtemos a corrente que passa pelo indutor, para obtermos a tensão basta utilizar a equação:

v t = L d i d t

Desse modo,

d i d t = - 5 * - 8 e - 8 t u t

Portanto,

v t = 1 2 * 40 e - 8 t u t

v t = 20 e - 8 t u t   V

Resposta

i t = 10 - 5 e - 8 t u t   A

v t = 20 e - 8 t u t   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na questão já se tem as equações de tensão e corrente, então a partir delas, deduzir algumas informações dos circuitos, bora resolver?
Depois de a chave no circuito da Figura P7.35 estar aberta por um longo tempo, ela é fechada em t = 0. Calcule (a) o valor inicial de i; (b) o valor final de i; (c) a constante de tempo para t ≥ 0 . (
A chave do circuito mostrado na Figura P7.36 esteve na posição a por um longo tempo antes de passar para a posição b em t = 0. a) Determine as expressões numéricas para i L(t) e vo (t) quando t $ 0. b
A chave do circuito mostrado na Figura P7.37 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. a) Determine a expressão numérica para i o (t) quando t $ 0.
A corrente e a tensão nos terminais do indutor no circuito da Figura 7.16 são i(t) = (4 + 4e-40t ) A, t $ 0; v(t) = -80e-40t V, t $ 0+. a) Especifique os valores numéricos de Vs , R, Io e L. b) Em qua