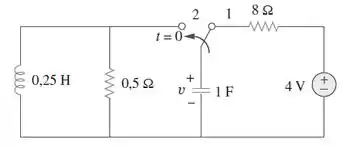
No circuito da Figura , a chave se encontra na posição há um longo tempo, porém, muda para a posição em .
- para .
Passo 1
Galerinha, na letra (a) queremos a equação característica do circuito. Bom, seja a tensão no capacitor e a corrente no indutor. No tempo , a chave está na posição e o circuito em regime permanente, logo o capacitor se comporta como circuito aberto e o indutor como um fio. Portanto,
Quando , o momento seguinte a troca de posição da chave, nós continuamos a ter . O circuito passa a ser:
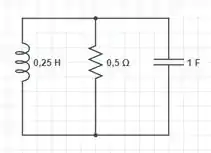
Assim, é igual a:
Passo 2
Na letra (b) queremos para . Nessa situação, temos um circuito RLC paralelo sem fontes. Vamos calcular e agora, para podermos escrever nossa equação característica!
Logo,
Portanto, a da tensão será igual a:
Para
Se derivarmos a expressão para , teremos:
Quando ,
Nos levando a resposta final,
Resposta
- e