Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 1

Para o circuito da Figura 8.62, determine:

(a) i ( 0 + ) e v ( 0 + )

(b) d i ( 0 + ) / d t e d v ( 0 + ) / d t

(c) i ( ∞ ) e v ( ∞ )

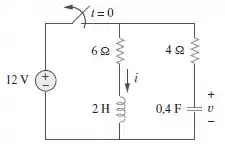
Passo 1

Primeiro vamos analisar o circuito antes da chave abrir, ou seja, t = 0 - .

Note que, o capacitor pode ser tratado como um circuito aberto, eliminando o resistor de 4 Ω , e o indutor como um curto-circuito. Assim,

o   c i r c u i t o   e q u i v a l e n t   e   :

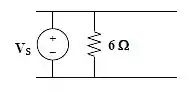
Por meio da lei de Ohm temos:

i 0 - = V s R = 12 6

i 0 - = 2 A

e,

v 0 - = 12 V

Passo 2

Certo! Agora vamos analisar quando a chave abrir, ou seja, para t = 0 + . Observe que o circuito equivalente vai ficar,

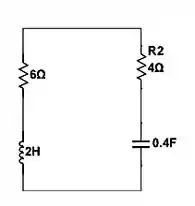
Lembre-se que, no indutor não pode haver mudança abrupta de corrente, e no capacitor uma mudança abrupta de tensão. Desse modo,

i 0 + = i 0 - = 2 A

v 0 + = v 0 - = 12   V

Passo 3

Para o item b) ainda continuaremos analisando o circuito quando a chave está aberta. Lembre-se que,

v L = L d i d t

Logo,

d i d t = v L L

Vamos aplicar a LKV, lei das tensões de Kirchhoff, obtemos:

v L 0 + - v 0 + + 10 i 0 + = 0

v L 0 + - 12 + 10 * 2 = 0

v L 0 + =   - 8 V

Portanto,

d i ( 0 + ) d t = v L L =   - 8 2 =   - 4   A / s

Passo 4

Similarmente, temos

i c = C d v d t

ou,

d v d t = i c C

Como,

i c 0 + = i 0 - =   - 2

Obtemos

d v ( 0 + ) / d t = - 2 0.4 = - 5   V / s  

Passo 5

Note que, como o circuito não tem uma alimentação externa quando a chave está aberta, então:

i ∞ = 0   A

v ∞ = 0   V

Resposta

  1. i 0 + = 2 A

    2.                                       v 0 + = 12   V

d i ( 0 + ) d t =   - 4   A / s

d v ( 0 + ) / d t = - 5   V / s

c)

i ∞ = 0   A

v ∞ = 0   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da Figura 8.92 , determine v ( t ) e i ( t ) para t0 . Suponha que v 0 = 0V e i 0 = 1A .
Após estar aberta por um dia, a chave do circuito da Figura 8.99 é fechada em t = 0 . Determine a equação diferencial descrevendo i ( t ) , t0 .
No circuito da Figura 8.102 , determine i ( t ) para t0 .
Considere a Figura 8.100 e elabore um problema para ajudar outros estudantes a entenderem melhor os circuitos de segunda ordem gerais.
O interruptor da Figura 8.105 se encontrava na posição 1 para t0 . Em t = 0 , ela muda instantaneamente para o terminal superior do capacitor. Observe que o interruptor fecha um contato (no terminal d