Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 48

Determine V_x ( s ) no circuito da figura.

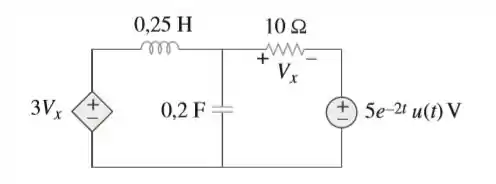
Passo 1

Primeiro, nós precisamos passar o circuito para o domínio de Laplace (s):

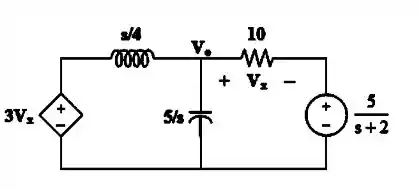
Passo 2

Após isso, vamos fazer a análise nodal no nó V_o :

(V_o - 3 V_x)/((s)/(4)) + (V_o - 0)/((5)/(s)) + (V_o - (5)/(s + 2))/(10) = 0

40 V_o - 120 V_x + 2 s^2 V_o_ + s V_o - (5 s)/(s + 2) = 0

( 2 s^2 + s + 40 ) V_o - 120 V_x - (5 s)/(s + 2) = 0

Mas como V_x = V_o - (5)/(s + 2)

Então, V_o = V_x + (5)/(s + 2)

Passo 3

Com isso, substituímos o V_o na equação da análise nodal e achamos V_x ( s ) !

( 2 s^2 + s + 40 ) (V_x + (5)/(s + 2)) - 120 V_x - (5 s)/(s + 2) = 0

2 ( s^2 + 0.5 s - 40 ) V_x = - 10 (( s^2 + 20 ))/(s + 2)

V_x ( s ) = - 5 (( s^2 + 20 ))/(( s + 2 ) ( s^2 + 0.5 s - 40 ))

Note que aqui a gente não precisa fazer inversa nem nada, porque o enunciado só pede a tensão no domínio de Laplace (s) e não no domínio do tempo!

Resposta

V_x ( s ) = - 5 (( s^2 + 20 ))/(( s + 2 ) ( s^2 + 0.5 s - 40 ))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha a função de transferência H ( s ) = V o V s para o circuito da figura.
Determine I 1 ( s ) e I 2 ( s ) no circuito da figura:
Considere o circuito com AOP da figura e determine v o ( t ) para t0 . Suponha que v s = 3 e - 5 t u ( t ) V .
Calcule o ganho H ( s ) = V o V s no circuito com AOP.
Um circuito tem a função de transferência a seguir H ( s ) = s + 4 ( s + 1 ) ( s + 2 ) 2 Determine a resposta ao impulso.