Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 42

No circuito da Figura P8.42, o resistor é ajustado para amortecimento crítico. A tensão inicial no capacitor é 15   V e a corrente inicial no indutor é 6   m A .

a) Determine o valor de R .

b) Determine os valores de i e de d i / d t imediatamente após o fechamento da chave.

c) Determine v c ( t ) para t ≥ 0 .

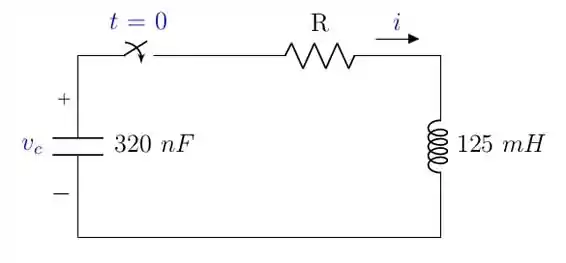
Passo 1

Show de bola, galera! Vamos continuar nossa saga do vaqueiro que é resolver circuitos transitórios.

a)

Para encontrar o valor de R , temos que encontrar primeiro a frequência de ressonância:

ω 0 = 1 L C ⇒ ω 0 2 = 1 L C = 1 125 ⋅ 10 - 3 × 320 ⋅ 10 - 9 ⇒ ω 0 2 = 25 ⋅ 10 - 6 r a d 2 s 2

Vale lembrar que quando a resposta é criticamente amortecida, temos que ω 0 2 = α 2 :

ω 0 = α = R 2 L = 5000 r a d s

⇒ R = 2 ⋅ 5000 ⋅ 125 ⋅ 10 - 3 ∴ R = 1250   Ω

Passo 2

b)

O valor de i ( 0 ) já é dito no enunciado, assim:

i 0 = 6   m A

Para encontrarmos d i / d t , vamos usar a equação da tensão no capacitor. Para isso, temos que conhecer v L . Isso será feito usando a LKT:

v L ( 0 ) = v C ( 0 ) - v R ( 0 ) = 15 - 1250 × 0,006 ⇒ v L ( 0 ) = 7,5   V

Assim

v L 0 = L ⋅ d i 0 d t ⇒ d i 0 d t = v L 0 L = 7,5 125 ⋅ 10 - 3

∴ d i 0 + d t = 60 A s

Passo 3

c)

Como o regime é o do amortecimento crítico, a resposta do capacitor vai ser do tipo

v C = A 1 t e - α t + A 2 e - α t = A 1 t e - 5000 t + A 2 e - 5000 t

Escolhendo t = 0 , vamos obter

v C 0 = A 1 ⋅ 0 ⋅ e - 5000 × 0 + A 2 e - 5000 × 0 = A 2 ⋅ 1 ⇒ v C 0 = A 2 = 15   V

Derivando a expressão de v C vamos obter

d v C d t = A 1 1 ⋅ e - 5000 t + t - 5000 e - 5000 t + A 2 - 5000 e - 5000 t

Escolhendo t = 0 , vamos obter

d v C 0 d t = A 1 e - 5000 × 0 + 0 ⋅ - 5000 ⋅ e - 5000 × 0 + 15 - 5000 e - 5000 × 0

⇒ d v C 0 d t = A 1 - 75000

Além disso, a definição da corrente no capacitor é

i C = C ⋅ d v C d t

Então,

d v C 0 d t = i C ( 0 ) C

Olhando para a figura do enunciado, que repetiremos aqui, podemos perceber que a corrente que percorre o indutor o polariza no sentido contrário à polaridade do capacitor. Assim, podemos escrever a expressão anterior em função da corrente no indutor:

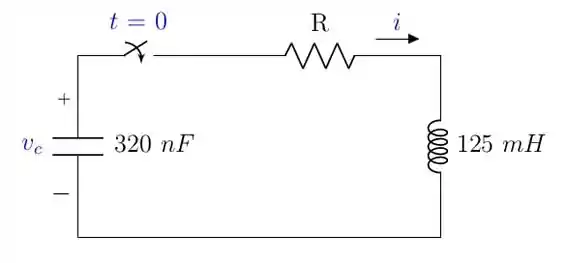
d v C 0 d t = - i L ( 0 ) C = - 0,006 320 ⋅ 10 - 9 ⇒ d v C 0 d t = - 18750

Logo,

d v C 0 d t = A 1 - 75000 ⇒ A 1 = - 18750 + 75000

⇒ A 1 = 56250 V s

Portanto,

v C t = 56250 ⋅ t ⋅ e - 5000 t + 15 ⋅ e - 5000 t   V ,     t ≥ 0

Resposta

a)

R = 1250   Ω

b)

i 0 = 6   m A                         e                      d i 0 + d t = 60 A s

c)

v C t = 56250 ⋅ t ⋅ e - 5000 t + 15 ⋅ e - 5000 t   V ,     t ≥ 0

Exercícios de Livros Relacionados

Assuma que R = 6Ω , L = 1H , v g = 0 , v 0 = 8V e i 0 = 4A na fig 9.10. Calcule i para t0 , se C éa) 1 5 F b) 1 34 F c) 1 9 F
Obtenha um filtro passa-faixa ativo usando a configuração do Prob. 15.4 , com f 0 = 1000H z , Q = 10 e K = 2 , com capacitores de 0,01 μ F . (Sugestāo: Ver Prob. 15.10.)
Calcule i , t0 , se v (0) = 6 V e i (0) = 2 A
Calcule i para t0 , se i g = 10A e o circuito está em regime permanente em t = 0 - .
A resistência no Problema 8.1 é reduzida para 80Ω . Determine a expressão para v(t) quando t ≥ 0 .