Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 56

Para o circuito mostrado na Figura 7.122, determine v ( t ) para t >   0 .

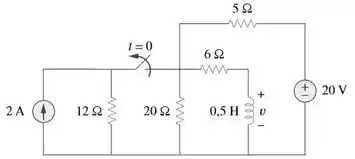
Passo 1

Calma galerinha, não priemos cânico! Cheio de coisa mas vamos destrinchar por partes!

Primeiramente, vamos calcular a resistência equivalente

R e q = 6 + 20   | | 5 = 10   Ω

τ = L R = 0.05

Então passando pra nossa equação padrão:

i t = i ∞ + i 0 - i ∞ e - t τ

A parte interessante desse paso é que o i ( 0 ) é encontrado aplicando uma analíse nodal para o circuito abaixo!

2 + 20 - V x 5 = V x 12 + V x 20 + V x 6 → V x = 12   V  

i 0 = V x 6 = 2   A

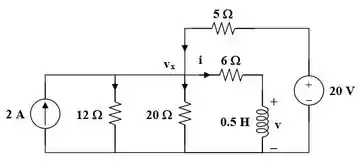
Passo 2

Legal? Agora, partindo de que 20 | | 5 = 4 ,

i ∞ = 4 4 + 6 4 = 1.6   A

i t = 1.6 + 2 - 1.6 e - t / 0.05 = 1.6 + 0.4 e - 20 t

Logo,

v t = L d i d t = 1 2 0.4 - 20 e - 20 t

v t = - 4 e - 20 t   V

Resposta

v t = - 4 e - 20 t   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando SPICE, calcule (a) i L 0 - ; (b) um gráfico de i L para 0 t30 μ s .
Em um circuito RL serie sem fontes, a corrente é i = 8 e - 5 t A e a tensão sobre o resistor é v = 32 e - 5 t V . Se a corrente entra pelo terminal positivo da tensão, calcule R, L, e a energia inicia
Calcule i para t0 , se o circuito está em regime permanente em t = 0 - .
O circuito mostrado está em regime permanente cc em t = 0 . Calcule v para t0.
Calcule i para t0 , se o circuito está em regime permanente em t = 0 -