Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 42

Considere o circuito da figura e determine i ( t ) e v ( t ) para t > 0 .

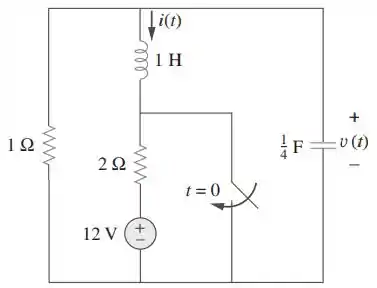
Passo 1

Vamos começar passando os elementos para o domínio de Laplace.

Passo 2

Fazendo análise nodal no nó V:

( V – 0 ) 1   +   V – 4 s 4 s   +   V - 0 s - 4 s =   0

e

I ( s ) = V - 0 s -   4 s

Passo 3

Separando em frações parciais teremos:

V ( s )   = ( 4 s + 16 ) ( s + 2 ) 2 = A s + 2 + B ( s + 2 ) 2

Agora basta encontrar A   e   B   :

A = 4

B = 8

Fazendo a inversa, temos:

v ( t )   =   4 e - 2 t + 8 t e - 2 t   V , para t > 0.

Daí, substituindo o V ( s ) na equação do I ( s ) :

I ( s )   =   4 s ( s + 2 ) + 8 s ( s + 2 ) 2 - 4 s

Por Laplace utilizando a tabela de transformadas, teremos:

i ( t ) = [ - 4 e - 2 t - 4 t e - 2 t ] u ( t )   A

Resposta

i ( t ) = [ - 4 e - 2 t - 4 t e - 2 t ] u ( t )   A

v ( t )   =   4 e - 2 t + 8 t e - 2 t   V , para t > 0.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine i ( t ) no circuito da figura por meio de transformadas de Laplace.
O capacitor no circuito da figura se encontra descarregado inicialmente. Determine v 0 ( t ) para t0 .
A resposta ao degrau de um circuito R L C é dada por d 2 i d t ² + 2 d i d t + 5 i = 10 ² Sabendo que i 0 = 6 e d i 0 d t = 12 , calcule i ( t ) .
Se R = 20Ω , L = 0,6H , qual o valor de C que torna o circuito:a) Superamortecidob) Criticamente amortecidoc) Subamortecido
A resposta ao degrau de um circuito R L C é v = 10 + 20 e - 300 t cos ⁡ 400 t - 2 s e n400 t V ,t ≥ 0 Quando o indutor é 50m H . Determine R e C .