Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 76
Considere o circuito da figura e determine . Suponha condições iniciais zero.
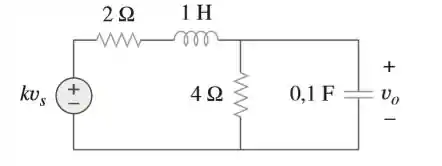
Passo 1
Vamos começar passando esse circuito para o domínio de Laplace (domínio s), incorporando as condições iniciais:
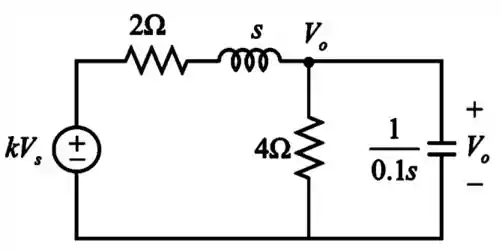
Passo 2
Usando a análise nodal, temos:
Agora, basta isolar nosso :
E então encontrar
Passo 3
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine a frequência central e a largura de banda dos filtros passa-faixa na Figura 14.88Letra b)
Determine a largura de banda e a frequência de corte do filtro rejeita-faixa da Figura 14.89.
Os parâmetros de circuito para um filtro rejeita-faixa R L C são: R=2k Ω , L=0,1H , C=40p F . Calcule:(a) A frequência central.(b) As frequências de meia potência.(c) O fator de qualidade.
Determine a transformada de Laplace de cada uma das seguintes funções:a) f ( t ) = t e - a t ;b) f ( t ) = s e n ω t ;c) f ( t ) = s e n ( ω t + u ) ;d) f ( t ) = t ;e) f ( t ) = c o s h ( t + u ) .
Use os teoremas do valor inicial e do valor final para verificar os valores inicial e final da corrente no Problema 12.28.