Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 12
Considere a Figura 10.61 e elabore um problema para ajudar outros estudantes entenderem melhor a análise nodal.
Passo 1
O problema pode ser proposto de inúmeros modos. Mas o escolhido é um exemplo, desse modo.
Por análise nodal, encontre no circuito da Figura abaixo:
Passo 2
O primeiro passo para resolver circuitos de corrente alternada é levar para o domínio da frequência, com isso temos:
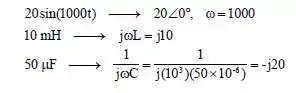
Desse modo o circuito fica,
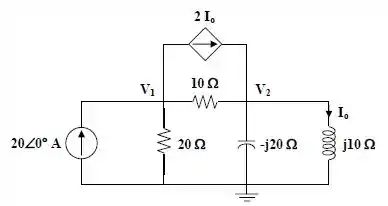
Passo 3
Agora vamos fazer a análise para cada nó. Portanto,
Para o nó 1,
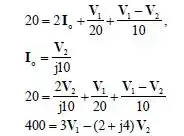
Para o nó 2,
Note que, temos 2 equações com duas variáveis, logo se substituirmos a segunda na primeira teremos,
Assim, levando de volta para o domínio do tempo temos
Resposta
Exercícios de Livros Relacionados
a) Para o circuito mostrado na Figura P9.31, determine a expressão de regime permanente para v o , se i g = 25 cos 50 . 000 tm A b) De quantos microssegundos é a defasagem entre v o e i g ?
O circuito mostrado na Figura P9.35 está em regime permanente senoidal. Determine o valor de ω , se i 0 = 40 sin ω t + 21,87 °m A , v g = 40 cos ω t - 15 °V .
Determine a expressão de regime permanente para v 0 no circuito da Figura P9.34, se i g = 1 60 cos 10.000 tm A .
Determine I b e Z no circuito da Figura P9.32, se V g = 25∠0 °V e I a = 5∠90 °A .
Use o método das correntes de malha para determinar o fasor corrente I g no circuito da Figura P9.55.